なぜパソコンでは2進法を使うのか
2進法について解説します。 皆さんは日常的に0から9までの10種類の数字によって数を表す10進法を使っていますが、 コピュータの内部では0と1の2種類の数字だけで数を表す2進法を使って計算が行われます。
動画でも解説しています。ご視聴いただいた後、本記事をお読みいただくと、より理解は深まります。
10進法では 「10」 になると繰り上がりが発生する一方、 2進法では「2」になると繰り上がりが発生します。 たとえば、
- 「10001」に1を足すと「10010」 (下1桁 [けた] について繰り上がり)
- 「10101」 に1を足すと 「10110」 (下1桁について繰り上がり)
- 「10111」 に1を足すと「11000」 (下3桁について繰り上がり)
- 「11111」に1を足すと 「100000」 (下5桁について繰り上がり)
となります。
これは10進法における以下の足し算と同じようなものです。 2進法で右から1が連続している部分を、 全部9に置き換えると分かりやすいと思います。
- 「10009」 に1を足すと「10010」
- 「10109」に1を足すと「10110」
- 「10999」 に1を足すと「11000」
- 「99999」に1を足すと 「100000」
この規則に従って、0から20までの数を数えてみると、次の表の通りになります。
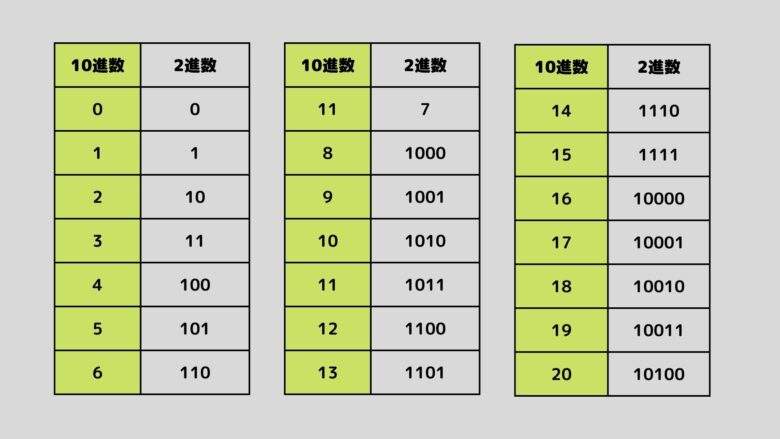
次に、 2進法を10進法に変換するにはどうすれば良いのでしょうか。 ゼロから1つずつ数を足していくと時間がかかってしまいますが、実は位の性質を使うと、 効率的に変換することができます。
10進法の仕組み
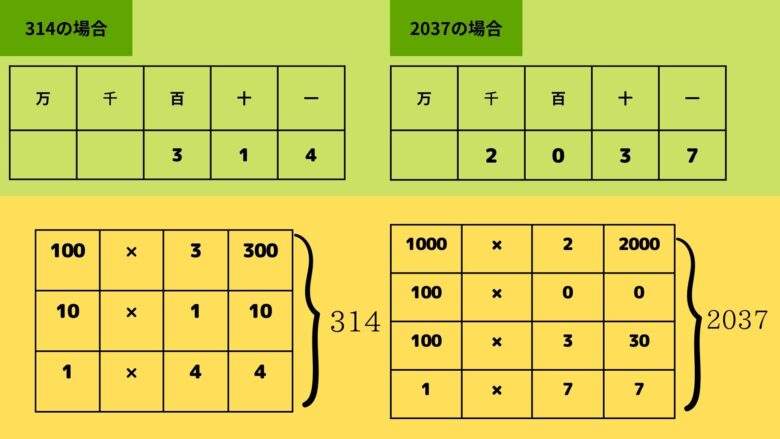
314の場合
ここで10進法の仕組みから解説しましょう。 10進法では下から順に一の位、十の位、 百の位、千の位、といったように桁に位が付けられ、 「位とその桁の数の掛け算」 の合計が元々の整数になります。
下図は314と2037の場合の例を示しています。
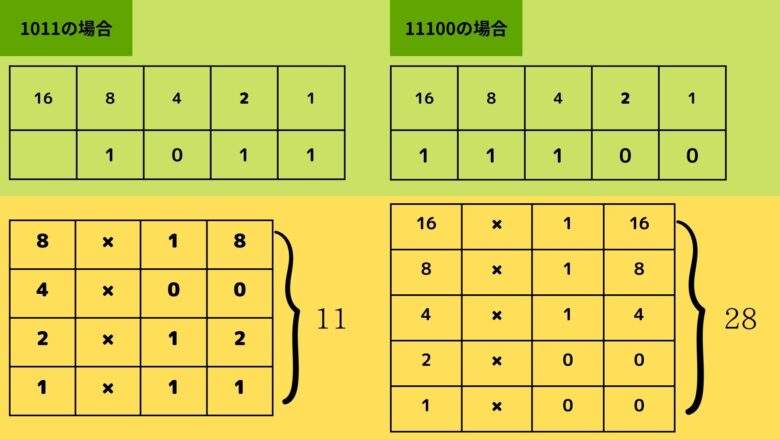
2進法→10進法の変換
2進法も同じような仕組みで動いています。 1を倍々していくと1→2→4→8→となるので、 1の位、2の位、4位、8の位、といったように桁に位を付けることを考えましょう。このとき、 「位とその桁の「数の掛け算」 の合計が2進法を10進法に変換した値になります。 たとえば1011を10進法に変換した値は1111100を10進法に変換した値は28です。
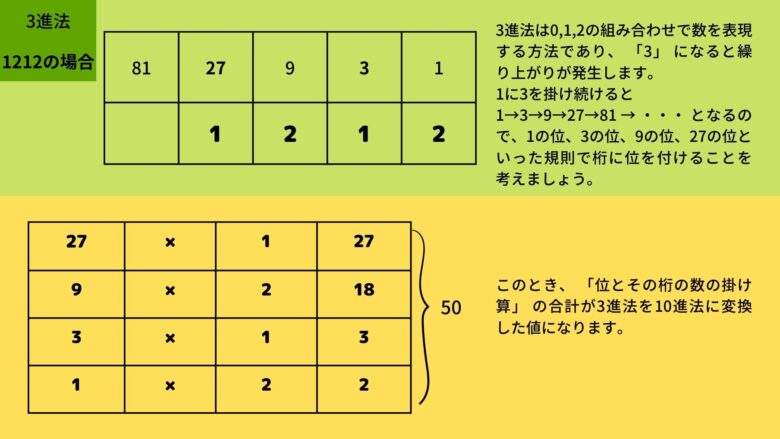
3 進法などについて
3進法は0,1,2の組み合わせで数を表現する方法であり、 「3」 になると繰り上がりが発生します。
そこで、1に3を掛け続けると1→3→9→27→81 → ・・・ となるので、1の位、3の位、9の位、27の位といった規則で桁に位を付けることを考えましょう。 このとき、 「位とその桁の数の掛け算」 の合計が3進法を10進法に変換した値になります。
たとえば3進法の1212を10進法に変換した値は50です。 また、3進法で 「abc」と書かれる数を10進法に変換した値は9a3b+cです。
4進法から10進法への変換
4進法は 0,1,2,3の組み合わせで数を表現する方法であり、「4」になると繰り上がりが発生します。
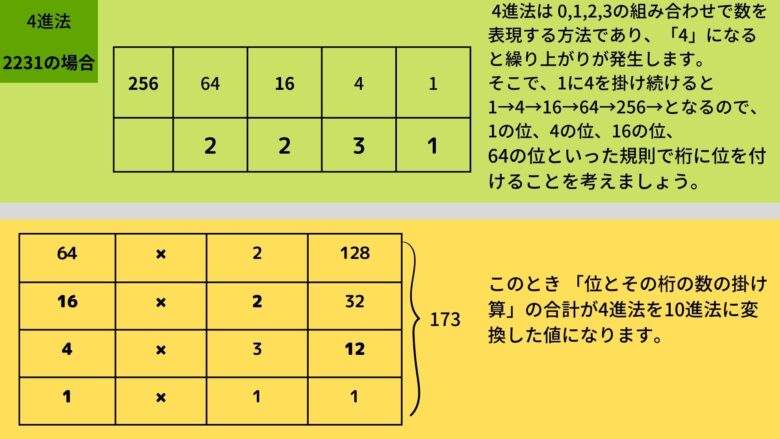
そこで、1に4を掛け続けると1→4→16→64→256→となるので、1の位、4の位、16の位、64の位といった規則で桁に位を付けることを考えましょう。このとき 「位とその桁の数の掛け算」の合計が4進法を10進法に変換した値になります。
たとえば4進法の2231を10進法に変換した値は173です。 5進法、6進法なども同様に定義され、同じような方法で10進法に変換することができます。
10進法から2進法などへの変換
下図のように「数がゼロになるまで2で割った余りを書いていき、それを下から読む」ことで10進法を2進法に変換することができます。
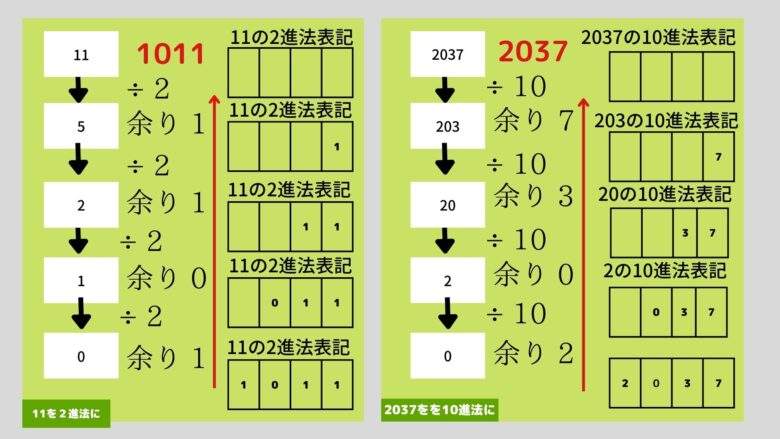
10進法を2進法以外に変換するときも同じような方法が使えます。 たとえば3進法の場合、 数がゼロになるまで3で割った余りを書いていき、それを下から読めば良いです。 下図右側の例のように、10進法を同じ10進法に変換する場合でも上手くいきます。
少し難しいですが、 この方法で上手くいく理由は、 2進法の未計算部分に着目すると理解しやすいです。
上図の左側の例について順を追って説明すると、以下のようになります。
- 最初に112は5余り1と計算しており、 11を2進法で表記した値 「1011」 の上3桁が、5を2進法で表記した値 「101」 と一致する
- 次に5÷2は2余り1と計算しており、 11を2進法で表記した値 「1011」 の上2桁が、 2を2進法で表記した値 「10」 と一致する
- 次に2÷2は1余り0と計算しており、 11を2進法で表記した値 「1011」 の上1桁が、 1を2進法で表記した値 「1」 と一致する
- 最後に、10進整数Nを入力し、2進整数に変換した値を出力するプログラムの例として、 コード4が考えられます。 ここでN% 2やN / 2などの 「2」 の値をすべて「3」 に変えたうえで適切に場合分けを行う
以上の手順で3進整数に変換することもできます。 4進法などその他の場合も同様です。
