計算回数を見積もろう
計算量(計算回数など)を見積もる方法について解説し、計算量の評価で重要な 「O(オー)記法」 の概念を導入します。
計算回数の重要性
あなたは「コンピュータ」 という言葉を聞いてどのようなイメージを思い浮かべるでしょうか。人間より圧倒的に計算速度が速く、いろいろな問題を解決できる万能な機械という印象を持っている人も多いでしょう。
実際、 人間が1時間かかる計算を、コンピューターはわずか100万分の1秒といった非常に短い時間で終わらせてしまいます。
しかし、コンピュータの計算速度にも限界があり、一般の家庭用コンピュータの場合、1秒間に約10億回しか計算できないことが知られています。
「効率の悪いアルゴリズム」 を使うと、少しデータサイズが大きくなれば簡単に計算回数が1京回 (1016回) を超え、残念ながら何時間待っても計算結果が出ません。
そのとき、頑張って書いた長大なプログラムが無駄になってしまうことでしょう。
したがって、プログラムを書く前に「どの程度の計算回数になるか」 「実際に動かしたらどの程度の時間で計算が終わりそうか」 を評価することが重要になってきます。
計算回数とは
計算回数は「答えが出るまでに行う演算の回数」 です。 たとえば、 1 +2 +3 +4 +5 +6を単純に1つずつ足していく方法で計算するときには、以下の5回の足し算を行うため、計算回数は5回です。
• 1+2=3 ,3+3=6 ,6+4=10, 10+5=15 ,15+6= 21
また、同じような方法で 1 +2 +3 +4 +5 +6 +7 + 8 を計算すると7回、 1+2+3+4+5+6+7+8+9+10 を計算すると9回の足し算を行います。
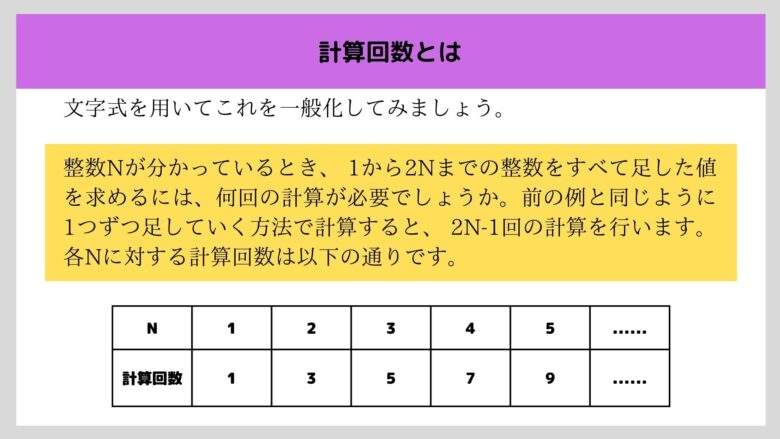
さて、文字式を用いてこれを一般化してみましょう。 整数Nが分かっているとき、 1から20までの整数をすべて足した値を求めるには、何回の計算が必要でしょうか。
前の例と同じように1つずつ足していく方法で計算すると、 2N-1回の計算を行います。各Nに対する計算回数は以下の通りです。
このようにシンプルな問題であれば正確な計算回数が分かるかもしれませんが、現実のプログラミングの問題はもっと複雑であり、2N-1の「-1」や「Nに付いている2」のような細かい部分まで正確に見積もるのは極めて困難です。 また、極限までプログラムを高速化しようとする場面を除き、2N回と3N回の違いはあまり重要ではありません。
そこで、「ざっくりN回の計算を行っている」 といったように、大まかな計算回数だけを見積もる考え方があります。
計算回数の例 ①: 定数時間
計算回数という概念に慣れるために、具体的な例をいくつか紹介します。
まずは以下の問題を考えましょう。

入出力を除くと、プログラムは以下のような計算処理を行っています。
・まず2*Nを計算する
・2*Nの結果と3を足し算する
N = int(input())
print(2 * N + 3)合計2回の計算を行っていますが、 大まかな回数のみを考える場面では2回も1回もそれほど変わらないので、計算回数は「ざっくり1回である」 ということができます。 このような計算回数になるアルゴリズムは定数時間であるといい、実行時間が入力データによらないなどの特徴があります。
計算回数の例 ②: 線形時間
次に、以下の問題を考えましょう。

この問題を解く方法として、たとえば 「1はXまたはY の倍数であるかどうか」 「2はXまたはYの倍数であるかどうか」・・・「NはXまたはY の倍数であるかどうか」 といった感じで1つずつ調べていくことが考えられます。このアルゴリズムは下のコードのように実装できます。

計算回数を理論的に見積もってみましょう。 for文ループの添字iが取り得る値は1,2,3,…,NのN種類であるため、 「計算回数はざっくりN回である」ということができます。
このような計算回数になるアルゴリズムは (Nに関して) 線形時間であるといい、 入力データの大きさが10倍、100倍に増えると実行時間が約10倍、100倍になるといった特徴があります。
なお、一重のfor文ループは、 このような計算回数になることが多いです。
計算回数の例 ③:全探索の計算回数
次に、以下の問題を考えましょう。

この問題を解くにあたって重要な知識を1つ紹介しましょう。 一般に、 あり得るすべてのパターンをしらみつぶしに調べる方法を全探索 (ぜんたんさく)といいます。 全探索は最もシンプルなアルゴリズムの1つであるため、問題を解く際には、まず全探索をしても現実的な時間で実行が終わるのかどうかを検討することが大切です。
さて、今回の2枚のカードの問題を全探索で解くことを考えます。 カードの書き方のパターン数をNの式で表すとN2通りであるため、計算回数は「ざっくりN2回である」ということができます。N2通りになる理由は、次の図のようにカードの書き方を正方形状に並べたときの大きさがN×Nになることを考えると理解しやすいです。

ここで本問題の制約は N1000であるため、最大でざっくり
1000 x 1000 = 106回
の計算を行う必要があります。 一方、家庭用コンピュータの計算速度は1秒当たり10回程度であるため、 次のようなコードを実装をすると、 2秒以内にプログラムの実行が終了するといえます。

プログラムの実行時間は、このような方法で見積もることができるのです。
計算回数がざっくりN2回となるアルゴリズムは、入力データの大きさが10、100倍に増えると実行時間が約100、10000倍になるといった特徴があります。
コンピュータの計算速度を考慮すると、N=10000程度であれば1秒以内で計算が終わるものの、N=100000以上になると時間がかかり過ぎてしまうことが分かります。なお、二重のfor文ループは、このような計算回数になることが多いです。
計算回数の例 ④: 全探索と指数時間
次に、少し設定を変えた以下の問題を考えましょう。

カードの選び方を全探索することを考えます。 このとき、調べるべきパターン数はどれくらいになるのでしょうか。 実際に数えてみましょう。
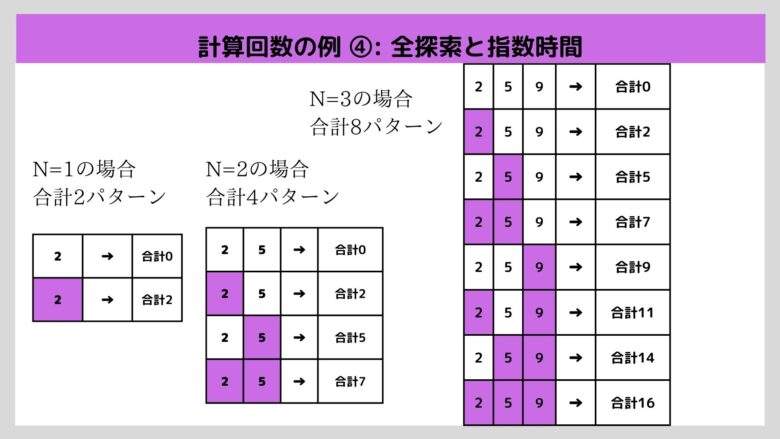
たとえばN=1の場合は「カード1を選ぶ」 「カード1を選ばない」 の2通りを調べれば良いです。 また、図に示すように、 N =2の場合は4通り、N=3の場合は8通りを調べる必要があります。 この程度の探索パターン数であれば、手計算でも容易に問題を解くことができるでしょう。
しかし、カードの枚数が少し増えると、急激にパターン数が増加します。N=4の場合は16通り、N=5の場合は32通りを調べなければなりません。この時点で、手計算で問題を解くのはかなり面倒でしょう。
それでは、探索パターン数をNの式で表してみましょう。Nが1ずつ増えると2→4→8→16→32・・と倍々に増えるので、Nに対するパターン数は以下の式で表されます。
2×2×2×2×2…..×2=2N
コンピュータは非常に高速な計算ができるので、32通り程度であればまったく問題ありません。しかし、さらにNを増やしてみるとどうでしょう。 探索パターン数は以下の通りであり、N=30以上では、さすがのコンピュータも 「指数関数」 の前には歯が立ちません。
さて、具体的にどのくらいの時間がかかるのでしょうか。 仮に1秒間に10個のパターンを調べ上げることができるとして計算すると、 この問題の制約の上限であるN=60では
260/109 ≒ 1.15*1018/109=1.15*109秒
かかります。 1年は約3200万秒なので、 実行が終わるのは32年以上後ということになります。 このような場面では、アルゴリズムを効率化する必要があります。
計算回数の例 ⑤二分探索と対数時間

すぐに思いつく方法としては、 「1以下ですか?」 「2以下ですか?」 「3以下ですか?」 といった順に、Yesが返ってくるまで質問していく方法でしょう。 たとえば「6以下ですか?」という質問で初めてYesが返ってきた場合、答えは6だと分かります。
しかし、この方法は効率が悪く、 たとえば太郎君の思い浮かべている数が8だった場合、 下図の通り8回の質問が必要です。
1以下ですか?
No
2以下ですか?
No
3以下ですか?
No
4以下ですか?
No
5以下ですか?
No
6以下ですか?
7以下ですか?
No
8以下ですか?
Yesどのようなケースでも3回の質問で答えを当てることができるのです。このような方法を二分探索法 (にぶんたんさくほう)といいます。
さて、少し問題設定を一般化してみましょう。

ランダウのO記法
「ざっくりN回」の代わりに「このアルゴリズムの計算量はO(N)である」、あるいは「このアルゴリズムはO(N) 時間で動作する」 ということができます。かなり難易度が高いですが、厳密に記述すると以下のようになります。

しかし、実用上はこのような難しいことを考える必要はありません。たいていの場合、計算量T(N) を表すO記法の中身P(N) は次の手順によって決められます。

なお、項の重要度は原則以下の順序に従うと思って良いです。 ただし、N!= 1 x 2 × 3× ・・・ xNです。
また、 アルゴリズムの計算量が、下図の赤色・黄色で示されているようなものの場合は指数時間である、下図の緑色・青色・灰色で示されているようなものの場合は多項式時間であるといいます。
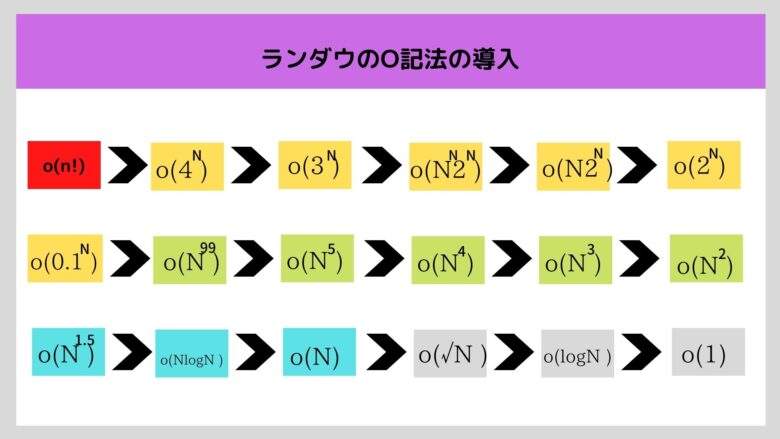
このような順序になる理由は、 N=1000などの大きい値を代入すると理解しやすいです。 たとえば計算回数がT(N) = N2+5Nの場合、各項の値は次のようになります。

次に、3つの具体例に対して計算量をO記法で表す過程を以下に示します。 なお、計算量オーダーの中身に対数関数が含まれる場合は、慣習的に O (log M) のように底を省略した形で書くことが多いです 。

計算量とアルゴリズムの例
以下の表は、典型的なアルゴリズムを、計算量ごとにまとめたものです。 さまざまな性能を持つアルゴリズムがあることが分かります。

計算量に関する注意点
計算量に関する注意点をいくつか記します。


計算回数とO記法の例題