このアルゴリズムの解説に自然数AとBの最大公約数を求める問題を扱います。 単純な方法で計算すると時間がかかってしまいます。 しかし、 ユークリッドの互除法を使うと、計算量O (log (A+B)) で答えが求められます。 アルゴリズムの紹介に加え、計算量にlogが出てくる理由を解説します。
最大公約数・最小公倍数
2つ以上の正の整数に共通する約数 (公約数) の中で最大のものを最大公約数といいます。たとえば6と9の最大公約数は3です。 これは6の約数が 「1,2,3,6」 9の約数が 「1,3,9」 であり、共通する最大の数は3であるからです。
一方、2つ以上の正の整数に共通する倍数 (公倍数) の中で最小のものを最小公倍数といいます。たとえば6と9の最小公倍数は18です。 これは6の倍数が 「6,12,18,24,309の倍数が 「9, 18, 27, 36,45,…」 と続き、 共通する最小の数は18であるからです。
2つの正の整数a,bには以下の性質が成り立つため、最大公約数と最小公倍数のうち片方でも分かれば、もう片方は簡単に計算することができます。
a x b = (aとbの最大公約数)×(aとbの最小公倍数)
そして最大公約数はユークリッドの互除法により効率的に計算することができます。

単純なアルゴリズム
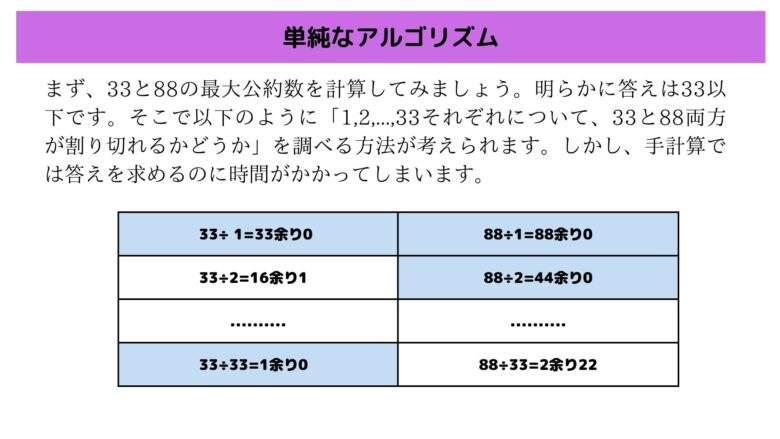
まず、33と88の最大公約数を計算してみましょう。明らかに答えは33以下です。そこで以下のように「1,2,…,33それぞれについて、33と88両方が割り切れるかどうか」を調べる方法が考えられます。しかし、手計算では答えを求めるのに時間がかかってしまいます。
最大公約数を求めるプログラム
一般の正の整数 A,Bの最大公約数についても、同じように1からmin (A,B) まで割り切れるかどうかを調べることで求められます。 たとえば次のコードのような実装が考えられます。 しかし余りの計算を 2 × min (A, B) 回行う必要があり、 あまり効率的ではありません。
# 正の整数 A と B の最大公約数を返す関数
# GCD は Greatest Common Divisor(最大公約数)の略
def GCD(A, B):
answer = 0
for i in range(1, min(A, B) + 1):
if A % i == 0 and B % i == 0:
answer = i
return answer
A, B = map(int, input().split())
print(GCD(A, B))効率的なアルゴリズム:ユークリッドの互除法
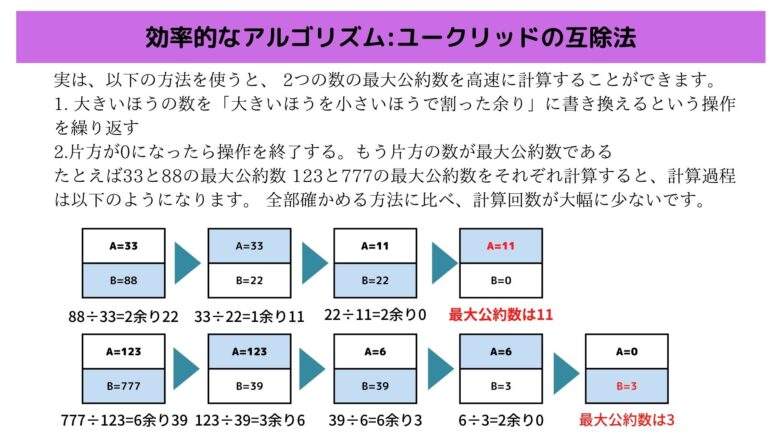
実は、以下の方法を使うと、 2つの数の最大公約数を高速に計算することができます。
たとえばこの方法で33と88の最大公約数 123と777の最大公約数をそれぞれ計算すると、計算過程は以下のようになります。 全部確かめる方法に比べ、計算回数が大幅に少ないです。
ユークリッドの互除法の実装例
このようなアルゴリズムをユークリッドの互除法といいます。 AとBの最大公約数を求めるときの計算量はO(log (A+B)) であるため、 A, B が 1018程度であっても一瞬で計算できます。
実装の一例としてコード3.2.2が考えられます。 AとBの大小関係によって行うべき操作が変わるので、
if文を用いて場合分けを行っています。 なお、 再帰関数 (3.6節) を用いた賢い実装方法もあります。
# 正の整数 A と B の最大公約数を返す関数
# GCD は Greatest Common Divisor(最大公約数)の略
def GCD(A, B):
while A >= 1 and B >= 1:
if A < B:
B = B % A # A < B の場合、大きい方 B を書き換える
else:
A = A % B # A >= B の場合、大きい方 A を書き換える
if A >= 1:
return A
returnB
A, B = map(int, input().split())
print(GCD(A, B))計算回数が log になる理由
次に、計算量がO (log (A+B)) になる理由を考えてみましょう。
まず、「1回の操作でA+Bの値が必ず2/3倍以下に減る」という重要な事実があります。たとえばA=33,B=88の場合の計算過程は次の通りであり、確かに2/3倍以下に減っています。
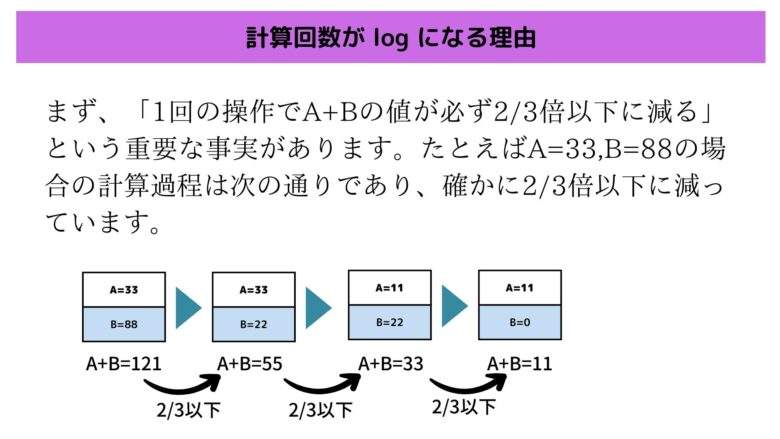
この事実はなぜ成り立つのでしょうか。 A<Bの場合はA,Bを逆にすれば良いので、ここではA≧Bの場合のみ考えます。
実は、 AとBの差が2倍以上かどうかによって場合分けを行うと、以下の理由により両方2/3倍以下に減っていることが分かります。
・差が2倍未満: 操作によってA+Bの値は 「3B未満」 から Bだけ減る
・差が2倍以上: 操作によってA+Bの値は 「3B以上」から「2B未満」に減る
たとえばBの値を10に固定して考えた場合は以下の通りです。 Aの値が20未満の場合も、 20以上の場合も、必ず2/3倍以下に減っています。
3個以上の最大公約数
3個以上の数の最大公約数も、ユークリッドの互除法によって計算することができます。 具体的なアルゴリズムの流れは次のようになります。
・まず、 1個目の数と2個目の数の最大公約数を計算する
・次に、前の計算結果と3個目の数の最大公約数を計算する
・次に、前の計算結果と4個目の数の最大公約数を計算する
……前の計算結果とN個目の数の最大公約数を計算する (この結果が答え)
たとえば24,40,60,80, 90, 120の最大公約数の計算過程は以下のようになります。なお、3項以上のビット演算と同様、計算順序を入れ替えても計算結果は変わりません。

