ビッグデータの解析には機械学習やディープ・ラーニングといった最先端のAI技術が必要で、それを使いこなすには数学的な感覚や知識が必要で……。わかって はいるけれど、何から勉強したらいいかわからない!
そんなみなさんの足がかりになればと思って書いた記事です。どうせなら数学とPythonを同時に学んでしまおうという、ちょっと欲張りな記事にしました。扱うテーマは中学 1 年生で習う「一次関数」です。その中から、「直線を表すグラフ」と「直線の式の求め方」を取り上げました。
いろいろな直線がどのような式で表されるのか、その式の一部を変えると直線は どう変わるのか、プログラムを書いて結果を確認しながら確実に理解を深めていき ましょう。数学が苦手な方でも、きっと「これならわかる!」と感じていただけると思 います。
逆に「簡単すぎて大丈夫?」と不安になる方もいらっしゃるかもしれませんが、基本を身につけた上で最後まで読み進めると、「機械学習」がどんなものか、ぼんやりと見えてくるはずです。
実行環境
■Jupyter Notebookをインストールする
記事のPythonプログラムは、Jupyter Notebookというツールを使って説明してい ます。このため、パソコンにあらかじめJupyter Notebookがインストールされて いる必要があります。Pythonプログラミングが初めての方は、(A)の方法で開発 環境を入手してください。すでにPythonがインストールされている方は、(B)を参
考にしてJupyter Notebookをインストールしてください。
(A)Anacondaのインストール
Anacondaのインストーラを下記のURLからダウンロードしてください。画面の指示 に従ってボタンをクリックするだけで、Python本体に加えてJupyter Notebookや 外部から提供されるライブラリを一括してインストールすることができます。
https://www.anaconda.com/products/individual
(B)Jupyter Notebookを個別にインストール
コマンドプロンプト(macOSの場合はターミナル)を起動して、次のコマンドを実行 してJupyter Notebookをインストールしてください。
> python -m pip install jupyter
また 、 グラフ描画 、数値計算 、 代数計算に外部ライブラリを使用します 。 次の3つのコマンドを実行してインストールしてください。
■Jupyter Notebookを起動する
Jupyter Notebookはプログラムの編集や実行、管理など、すべての作業を Webブラウザ上で実行できるツールです。WindowsにAnacondaをインストールし た方は、スタートメニューから[Anaconda3]→[Jupyter Notebook(anaconda3)] の順に選択してください。
pipコマンドでJupyter Notebookをインストールした方、 またはmacOSでAnacondaをインストールした方は、コマンドプロンプト(またはターミナル)から次のコマンドを実行してください。
> jupyter notebook
> python -m pip install matplotlib
> python -m pip install numpy
> python -m pip install sympy
しばらくするとご使用の環境で既定のアプリとして登録されているWebブラウザが 起動して、Jupyter Notebookの初期画面が表示されます。ここがJupyter Not ebookを利用する際のルートフォルダになります。
図Jupyter Notebookが起動したところ
■作業用のフォルダを作成する
Jupyter Notebookでプログラムを作る前に、作業用のフォルダを作っておきましょ う 。 画 面 右上にある
[ New ]を クリックして 、 表示されるメニューの中から「Fo l der」を選択してください。
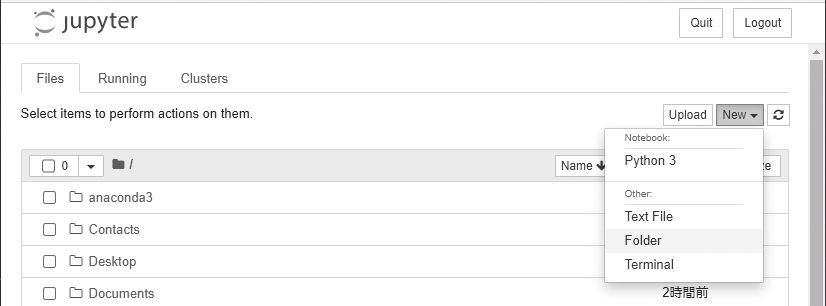
図 フォルダの新規作成
するとルートフォルダに「Untitled Folder」という名前のフォルダが作成されます。 作成時には名前を付けられないので、ここでフォルダ名を変更しましょう。フォルダ 名の左側にチェックを入れてから、画面左上の[Rename]をクリックすると、フォル ダ名を変更できます。「PythonSample」といったようにわかりやすい名前に書き換 えて、[Rename]をクリックしてください。変更後のフォルダ名をクリックすると、そのフォルダに移動します。
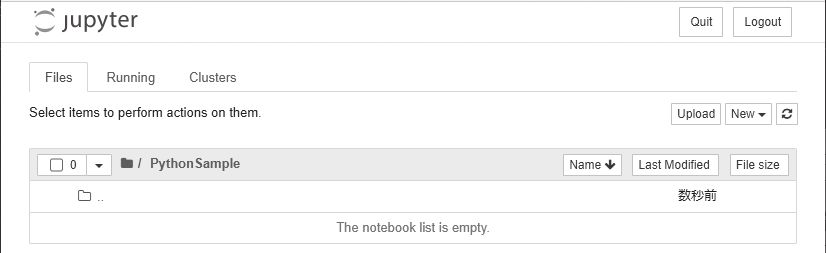
作業フォルダをクリックして開いたところ
■ Notebookを作成する
新たにプログラムを作るには、最初にNotebookを作成します。画面右上にある [New]をクリックして、メニューの中から「Python3」を選択してください。すると 新しいタブが開き、新しいNotebookが表示されます。このNotebookを使ってPythonのプログラムを編集します(図D)。新たに作成したNotebookは「Untitled」 という名前になっています。画面上で「Untitled」の部分をクリックすると名前を変 更できるので、わかりやすい名前に変更しておきましょう。なお、ここでの名前がNotebookのファイル名になります。
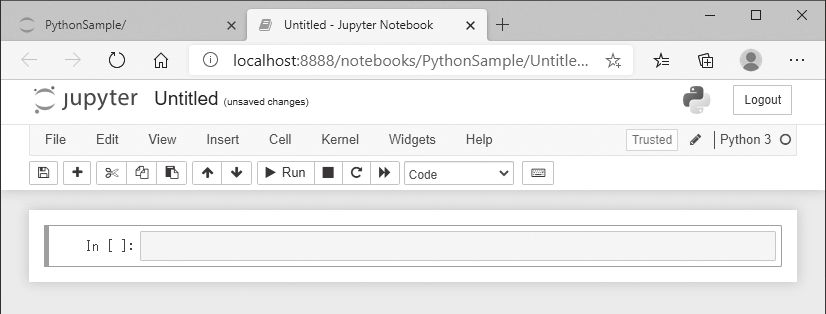
新しいタブで新規のNotebookが開く クリックすると名前を変更できる
■ Pythonプログラムを実行する
Notebookを開くと、「In [ ]」という表示で始まる項目が表示されました。この「In [ ]」の右横にある四角い箱を「セル」と言います。ここに、Pythonの命令を入力してください。対象のセルをクリックしてから、ツールバー上の[Run]をクリックすると、命令を実行して結果をセ ルの直下に表示します。一番下のセルを実行した場合は、新しいセルが 追加されます。
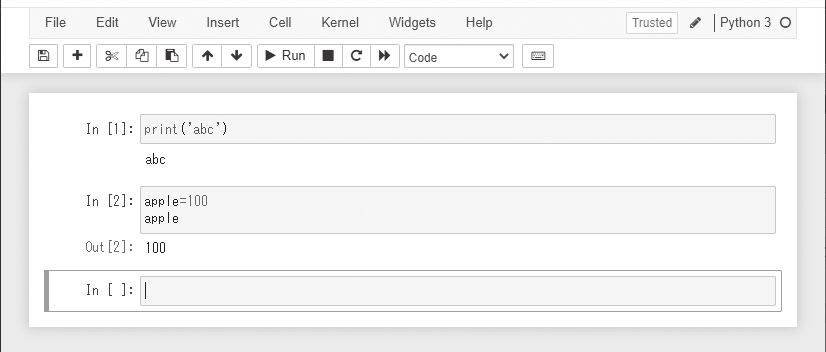
プログラムを実行 [Run]をクリックしてプログラムを実行
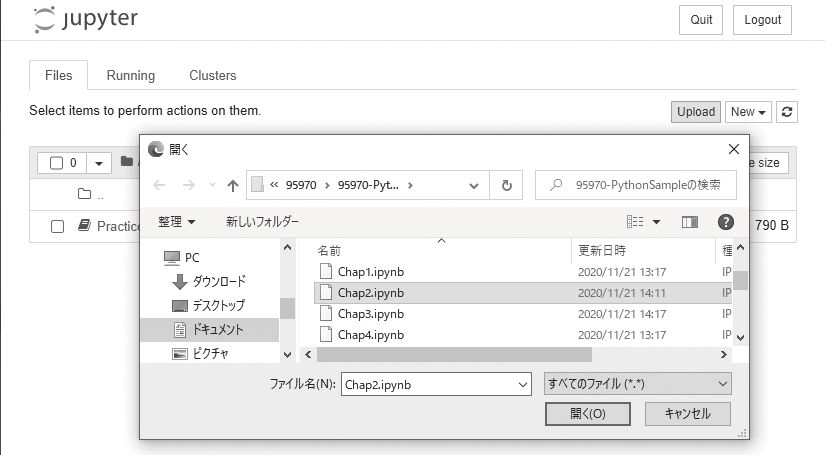
ダウンロードしたNotebookファイルを選択
ファイルを選択して[開く]を押す
直線とグラフ
「定規を使って、この紙に直線を引いてください」と言われたら、どんな直線を引きますか?
横にまっすぐ? 縦にまっすぐ? それとも斜め? 直線を引 くのは簡単ですね。
では、いま引いた直線を他の人に正確に伝えてください。
うまく伝えられますか? このときに役に立つのが数式です。数式を使えば、この直線を正確に伝えることができるだけでなく、誰でも同じ直線を再現することができるのです。ここからは直線がどのような数式で表されるのか、それをPython のプログラムで確かめていきましょう。
たとえば、図 1-1 の直線を定規で引いたとします。あなたならこの直線をどう説明しますか? 「右上がりの直線」では説明不足です。なぜなら「右上がり」と言っても、傾き具合の受け取り方は人によっていろいろだからです。
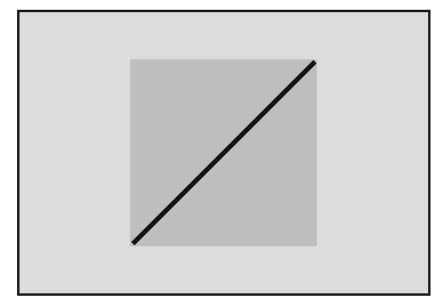
図1-1 適当に引いた直線
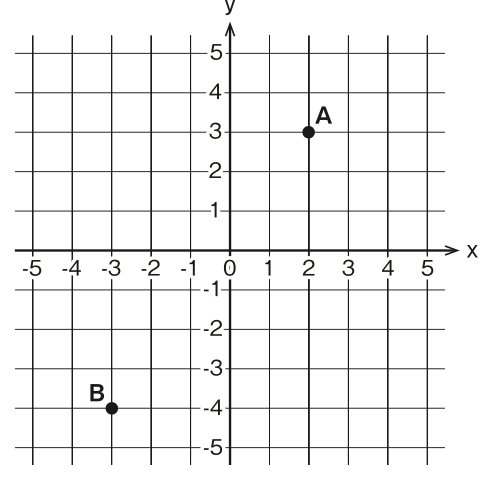
この直線を正しく伝えるために、「直交座標系」を用意しましょう。こういうと難しそうですが、言ってみればグラフのように扱うことで、正確に直線を表そうということです。 直交座標系とは横の軸をx、縦の軸をyとして、両方の座標軸が垂直に交わる座標系です。x 軸は左から右、y 軸は下から上が正方向、つまり値が大き くなっていく方向です。この座標系を使うと、平面上の点は (x,y)で表すことができます。
たとえば、図1-2の点Aは(2, 3)、点Bは(-3, -4)です。
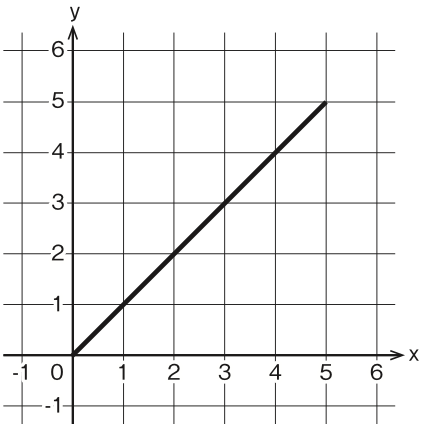
さて、図 1-1 で引いた直線を座標系に重ねてみると……直線上の座標が いくつか読み取れるようになりました。
図1-3 さっきの直線を座標系に重ねると……
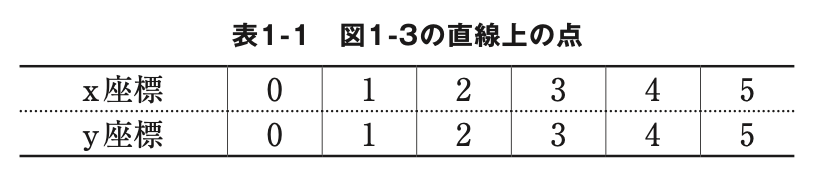
読み取れた点を書き出したものが表 1-1 です。x 座標とy 座標が同じ値です ね。ということは、この直線はy=x という式で表すことができそうです。
Matplotlibでグラフを描く
「私が描いたのはの直線です」と説明したら、目を白黒させる人がいるかもしれませんが、一方で数学の得意な人ならあなたが描いた直線を見なくても、このひと言で同じ直線を思い浮かべることがで きます。数式で表されているのですから、コンピュータでも再現できるはずです。やってみましょう。
プログラム1-1は y=xで表されるグラフを、 xの値が0から5の範囲で描くプログラムです。新しい Notebook を開いて、最初のセルにこのプログラムを入力してみてください。
プログラム1-1
%matplotlib inline
import matplotlib.pyplot as plt
x = [0, 1, 2, 3, 4, 5]
y = x 6
plt.plot(x, y)
plt.show()
では、プログラムを上から順に見ていきましょう。1行目はPython の命令ではなく、セルの直下にグラフを表示するためのJupyter Notebook の命令です。このため、実質 2 行目からが Python のプログラ ムです。その 2 行目を見てください。
グラフの描画には Matplotlib パッケー ジ内の Pyplot モジュールを使うので、最初に import matplotlib.pyplot as plt を実行して、Matplotlib.Pyplot モジュールに plt という名前を付けて読み込んでおきましょう。点や直線を描画する命令を利用するときに、 「matplotlib.pyplot」と書く代わりに「plt」だけで呼び出せるようになります。
4 行目でリスト型の変数 x に 0 から 5 までの値を代入しておいて、5 行目に直線を表す式と同じ を記述しています。プログラムの中でイコール( )は代入という意味なので、これで変数yにはxと同じ 値が代入されます。7 行目の plt.plot(x, y)は、与えられた座標を線でつなぐ命令です。
xとyにはそれぞれ[0, 1, 2, 3, 4, 5]という値が代入されているので、この命令で(0, 0)と(1, 1)、(1, 1) と(2, 2)、(2, 2)と(3, 3)、(3, 3)と(4, 4)、(4, 4)と(5, 5)の間を結ぶ線を引くことができます。最後の show( ) は描画した内容を画面に表示する命令です。
このプログラムを実行すると、図 1-4 のグラフが表示されます。確か に右上がりの直線になりました。でも、図 1-3 の直線よりも傾きが緩や かです。表 1-1 と同じ座標を使ったのに同じ直線にならないなんて、納 得できませんね。
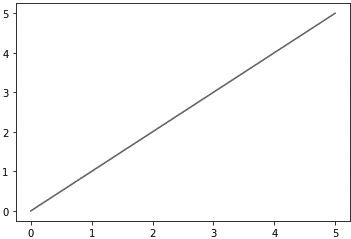
図1-4 プログラム1-1の実行結果
グラフを描画した領域を「プロット」と言いますが、この大きさは プログラムの中で特に指定しない限り、図 1-4 のような横長になりま す。
また、プロットの中にグラフ全体が収まるように、縦と横の目盛りも自動的に調整されます。図 1-4 をよく見ると、横の目盛りのほうが縦 の目盛りよりほんの少し大きくなっていますね。その結果、直線の傾 きが緩やかになったのです。……と、その理由がわかっても、同じにならないのは気になります。 新しいセルを追加して、プログラム 1-2 を入力してください。
プログラム1-2 縦と横の目盛りを揃えて描画する
x = [0, 1, 2, 3, 4, 5]
y = x
plt.plot(x, y)
plt.axis(‘equal’)
plt.grid(color=’0.8′)
plt.show()
これは、縦と横の目盛りを揃えてグラフを描画するプログラムです。座標を 確認しやすいように、薄いグレーでグリッド(目盛りの補助線)も描画するよう にしました。それが 5 行目と6 行目です。これ以外はプログラム1-1と同じです。 このプログラムを実行すると図 1-5 のようになります。これなら図 1-3

と同じ直線だと納得できますね。
なお、axis()とgrid() は、これから表示するプロットの体裁を整える命令です。必ず show() の前に実行してください。
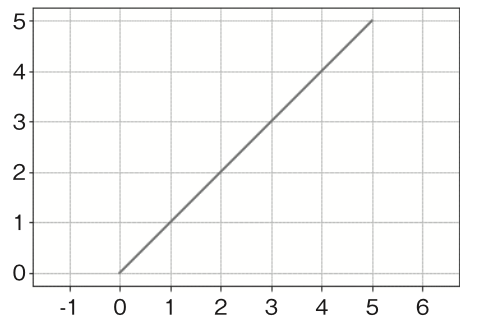
図1-5 プログラム1-2の実行結果
比例の式
y=xという式で直線を表せることがわかりました。ここから先はこの数式を変えることで直線がどう変わるのか、見ていきましょう。 ここに 1 リットル(L)のペットボトルがあるとします。これに水を 入れると重さは 1kg です。すると、水の入ったペットボトルの本数と 重さ(それぞれ とします)の関係は表 1-2 のようになります。
表1-2 1Lのペットボトルの本数と重さの関係

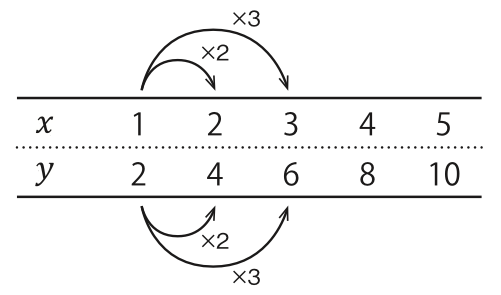
ここでペットボトルの本数をx 、重さをyとすると、表 1-1と同じ数が並びましたね。同じように 2L のペットボトルの本数と重さの関係を示したものが表 1-3 です。


xの値が2倍になると yの値も2倍、 が3倍になるとも3倍になっています(図 1-6)。 xが 2 倍だとyも 2 倍、3 倍のときも同様という点は、 表 1-2 も変わりません。
図1-6 と の関係
このように xと yが同じ割合で変化することを「 yは xに比例する」 と言い、 y=ax
という式で表します。 aは「比例定数」で、この値は式を変形するこ とで求められます( a=y/x)
さて、表 1-2 の場合、比例定数は 1 です。

「グラフから読み 取れる xとyの値が等しいから、図1-3の直線はy=axで表される」と 説明しましたが、本当は「 xとyは比例関係にあり、その比例定数は 1 である」というほうが、数学的により望ましい説明ということができ ます。
関数とグラフ
ここでもう一度、先ほどの比例の式を見てください。 y=axこの式では xの値が 1 つに決まれば yの値も 1 つに決まることから、 「 yは xの関数である」とも言えます。プログラム 1-1 とプログラム 1-2 では座標を直接与えてグラフを描画しましたが、同じ処理を 関数を使ったプログラムに書き換えてみようと思います。次のプログラムの最初の 2 行が関数の定義です。
プログラム1-3
def func_1(x):
return x
x = []
y = []
for i in range(0, 6): x.append(i)
y.append(func_1(i))
plt.plot(x, y)
plt.axis(‘equal’)
plt.grid(color=’0.8′) p
lt.show()
1行目はfunc_1という名前の関数を作る命令です。2行目のreturn 文で、受け取った引数 x をそのまま呼び出し元に返しています。これ で と同じ処理をする関数が定義できました。
4 ~8行目はxとyに値を代入する処理です。4 ~5行目であらかじめ空のリストを用意した後、6 行目の
for i in range(0, 6):
はiの値が0≦i<6の範囲、つまり0~5の間の繰り返すという意味です。 繰り返し区間の終了値は range() が作る連続する値に含まれないので 注意してください。
7 ~8行目のappend()は、リストに値を追加する命令です。つまり、 この繰り返し処理を完了すると、リストxには[0, 1, 2, 3, 4, 5]が、リス トyにはfunc_1()を実行した結果、同じように[0, 1, 2, 3, 4, 5]が代入さ れます。
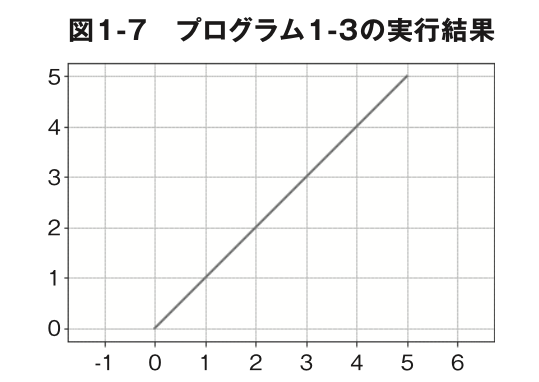
10 行目からはグラフを描画する命令です。プログラム 1-3 を実行す ると、プログラム 1-2 の実行結果(図 1-5)と同じグラフが表示されま す(図 1-7)。
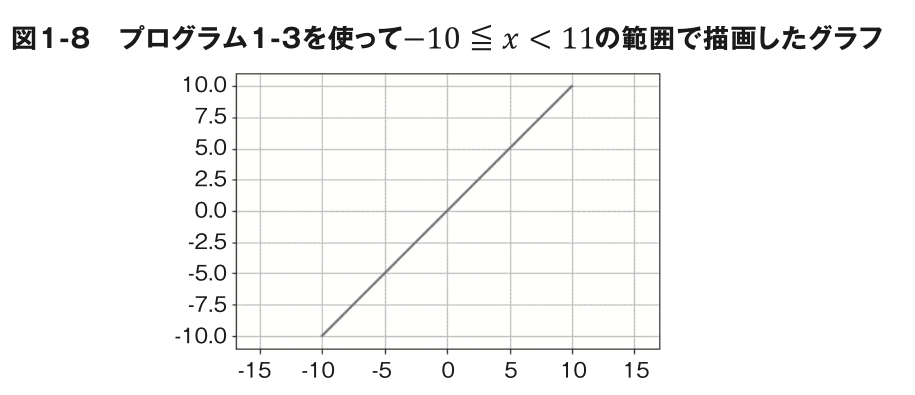
少し複雑なプログラムに見えるかもしれませんが、プログラム の便利なところはグラフの範囲を簡単に指定できるところです。たとえば、y=x のグラフを xの値が -10 ~ 10 の範囲で描画するときは for i in range(-10, 11): のように range() で区間を示す引数の部分を指定し直すだけです。これ で の範囲を変えたグラフを作成できます)。
プログラム 1-1 やプログラム 1-2 のように x に代入した座標をすべ て書き換えるよりも手軽ですね。もう1つ、関数にすると y=axの aの値を変えるのも簡単になります。 たとえば、2L のペットボトルの本数(x)と重さ(y)の関係は y=2xという式で表すことができるので、
def func_2(x):
return 2 * x
と関数を定義すれば xに対するyの値が求められます。プログラム 1-4 はこの関数を使ってグラフを描画するプログラム、図 1-9 はその結果 です。 y=xのグラフとの違いはどこだと思いますか?
プログラム 1-4
def func_2(x):
return 2 * x
x=[]
y=[]
fof i in range(0,6):
x.append(i)
y.append(func_(i)
plt.plot(x, y)
plt.axis(‘equal’)
plt.grid(color=’0.8′)
plt.show()
図1-9 プログラムの1-4実行結果
直線の傾きを決めるもの
ここまでで の式を使うと直線が引ける(グラフが描ける)ことがわかりました。図 1-10 のグラフを見てください。
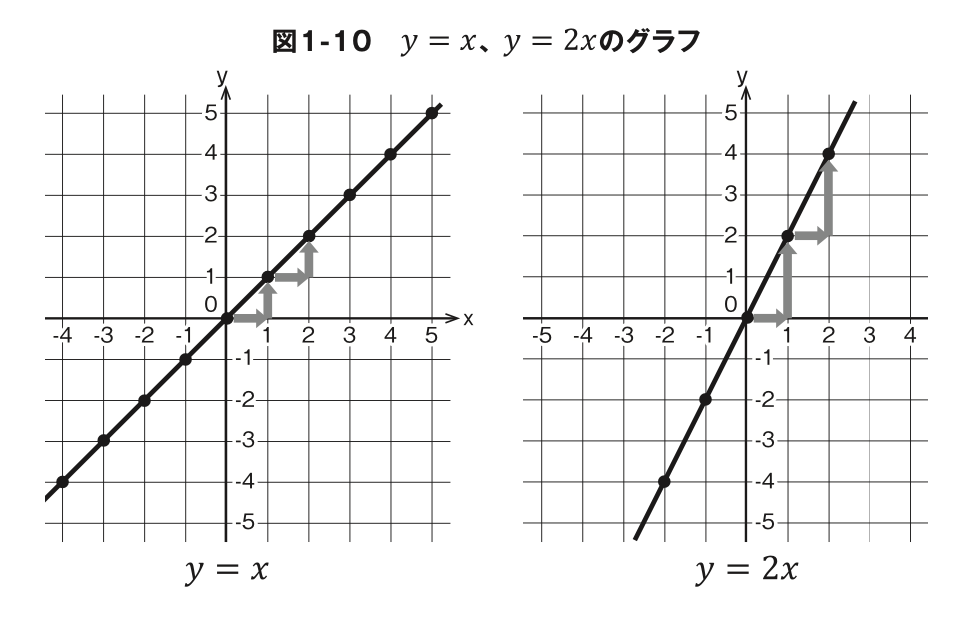
左は y=x、右はy=2xのグラフです。どうやら y=axのaの値が 変わると、傾きが変わるようです。 図1-10を見ると、直線の傾きが表しているのは「 xが1増えるときにyがどれだけ増えるかを表す値」と言えそうです。
そして、この値はグラフから読み取れますね。これを「変化の割合」と言うことにします。 y=xは xが 1 増えるとyも 1 増えるので変化の割合は 1、 y=2xのときは2増えるので、変化の割合は 2 です。この変化の割合 が直線の傾きになるのです。 なお、直線の傾きはつねに一定ですから、変化の割合はどこを調べても同じです。図 1-11 のグラフのように xが 1 増えたときに yがどれ くらい増えるか読み取りにくい場合は、 xの増分を変えてわかりやすいところを使いましょう。
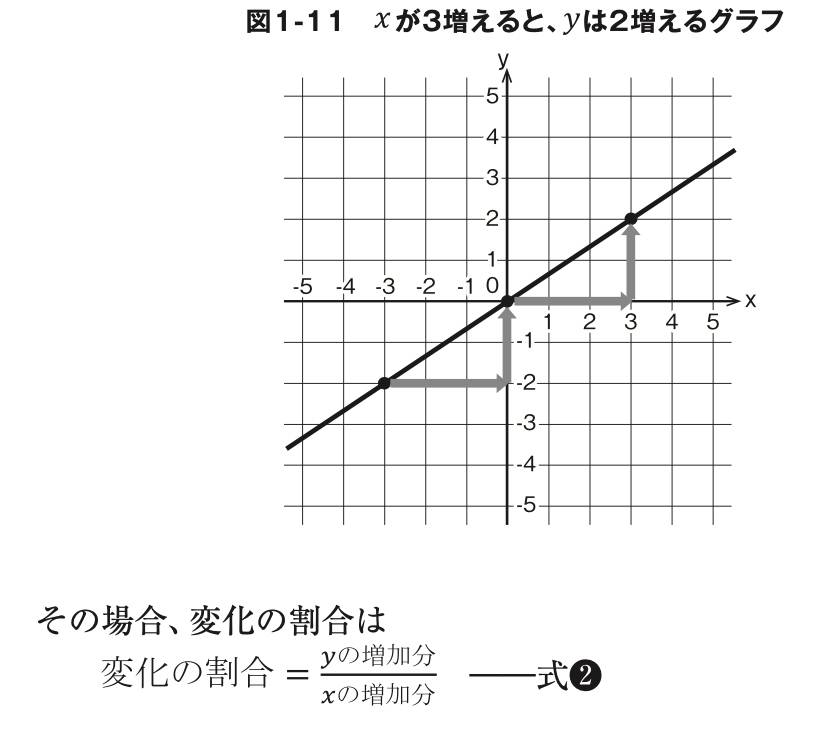
で求められるので、これに当てはめると図1-11の変化の割合は2/3 、つまりこの 直線を表す式はy=2/3xです。
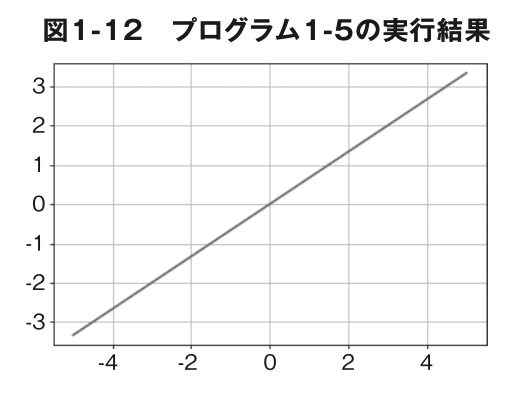
プログラム1-5 は、 y=2/3xのグラフを描画するプログラムです。 aの値が分数の場合でも 、関数の作り方 は同じです 。return文に式をそのまま書きましょう。
プログラム1-5 のグラフを作成
def func_3(x):
return 2/3*x
x=[]
y=[]
for i in range(-5,6):
x.append(i)
y.append(func_3(i))
plt.plot(x, y)
plt.axis(‘equal’)
plt.grid(color=’0.8′) 13. plt.show()
右下がりの直線
ここまでは右上がりの直線を見てきました。ここでは逆に右下がり の直線を見てみましょう。
図1-13は右下がりのグラフです。 xの値が3増えると yの値は2減っていることから、変化の割合は 、-2/3 です。このよう に y=axで a<0のとき、直線は右下がりになります。
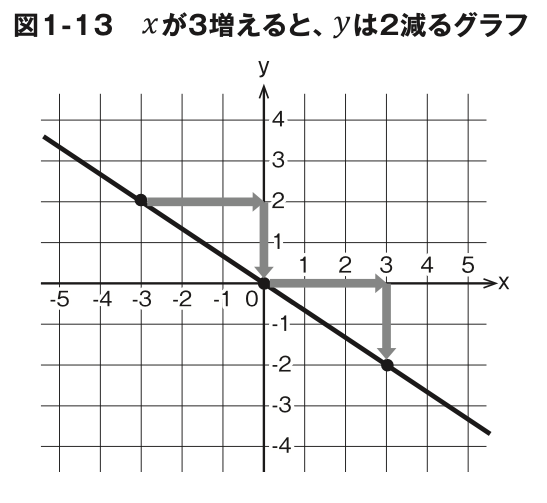
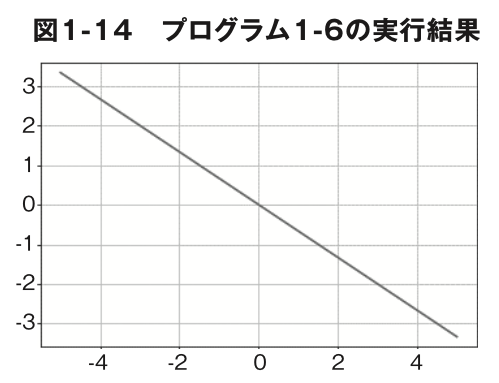
プログラム1-6は y=-2/3xのグラフを作成するプログラムで す。 aの値をいろいろ変えて、負の数のときは本当に右下がりの直線 になるか確認してみましょう(図 1-14)。
プログラム1-6
func_4(x):
return -2 / 3 * x
x=[]
y= []
for i in range(-5, 6):
x.append(i)
y.append(func_4(i))
plt.plot(x, y)
plt.axis(‘equal’)
plt.grid(color=’0.8′)
plt.show()
座標軸に並行な直線
ここまででわかったことは、
1 y=axを使って直線(グラフ)が描ける
2 aは直線の傾きを表す
3 a>0のときは右上がりの直線になる
4 a<のときは右下がりの直線になる
という4 点です。ここまでくるとa=0 のときにどうなるか、気になりますね。 プログラム1-7を実行して確認しましょう(図 1-15)。
プログラム1-7
def func_5(x):
return 0*x
x=[]
y=[]
for i in range(-5, 6):
x.append(i)
y.append(func_5(i))
plt.plot(x, y)
plt.axis(‘equal’)
plt.grid(color=’0.8′)
plt.show()
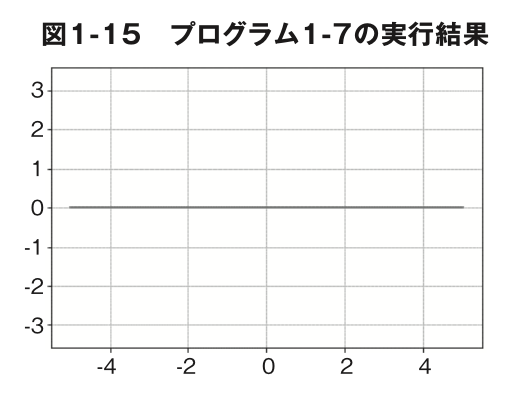
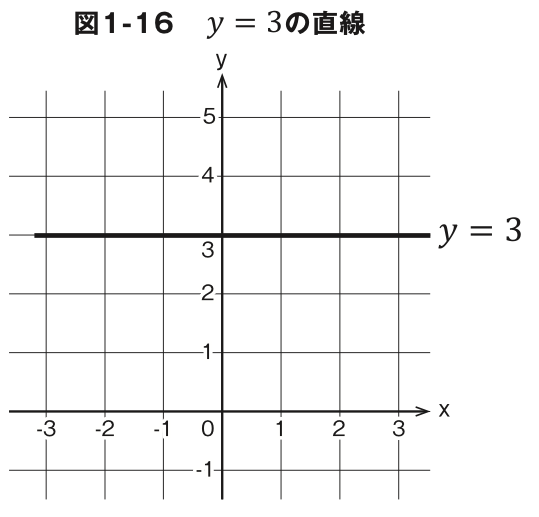
y=axで a=0のときは、 xがどんな値でも yの値は0にしかなりません。つまり、図 1-15 のようにx 軸に重なる直線になり、これを式で表すと y=0です。 では、y=3 はどんな直線になると思いますか? xがどんな値でも yの値は常に3です か ら 、これは y 軸 の 3を通ってx 軸と平行 な直線になります。
同じように考えるとy軸に重なる直線はどうなるでしょう。この場合、 yの値が どんなときも xの値は常に0ですから x=0です。同様に、x軸の3を通ってy 軸に平行な直線は x=3です(図 1-17)。
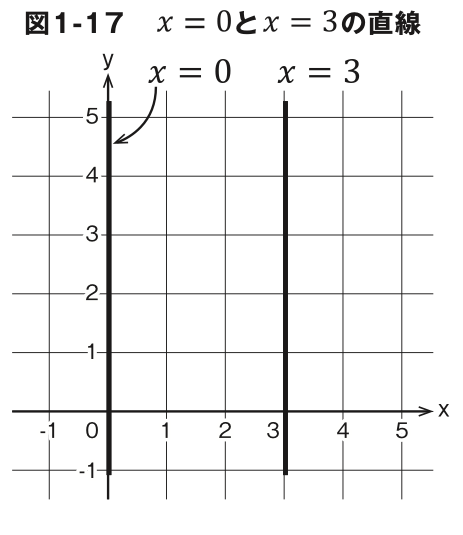
ただし、y 軸に平行な直線の式は関数ではありません。 xの値を増 やすことも、 yの値を1つに決めることもできないからです。
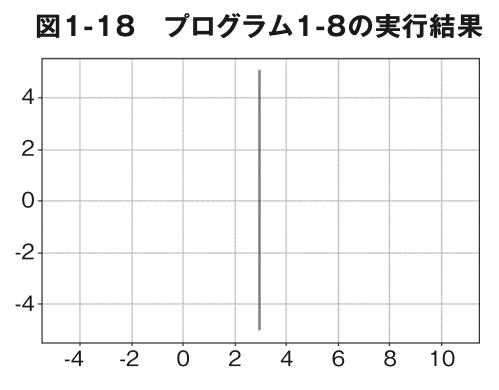
プログラ ム 1-8 は、 x=3のグラフを yの値が -5 ~ 5 の範囲について描画するプログラムです(図 1-18)。始点と終点の 2 つの座標があれば直線は描画 できるので、リスト型の変数 x と y にはそれぞれの座標を代入してください。x の値はつねに 3、y の値は区間の開始と終了です。
プログラム1-8
x = [3, 3]
y = [-5, 5]
plt.plot(x, y)
plt.axis(‘equal’)
plt.grid(color=’0.8′)
plt.show()
直線の位置を決めるもの
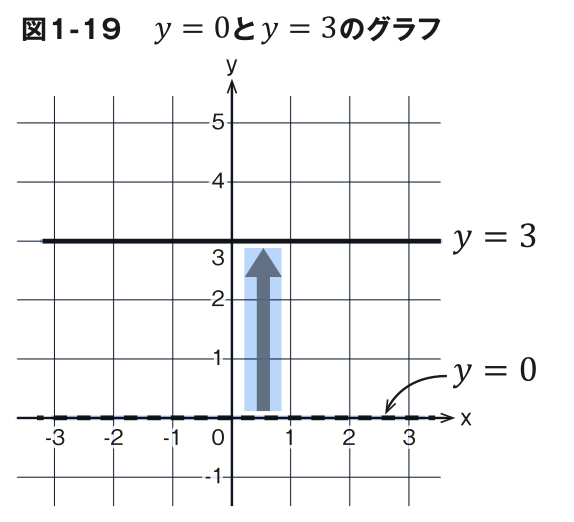
図 1-19 の点線は の直線です。この直線を y 軸の 3 を通るよう に平行移動すると、直線の式は y=3になります。
傾きのある直線も同じように考えることができます。図 1-20 の点線は y=2xの直線です。この直線を y 軸の 3 を通るように平行移動すると実線の位置になり、直線の式は y=2x+3になります。「なんだかだ まされた気がするぞ?」という人は図 1-20 から読み取れる座標を書き 出してみましょう(表 1-4)。実線上にある yの値は、同じ xの位置にある点線上の yよりも、どれも 3 ずつ大きな値になっていますね。
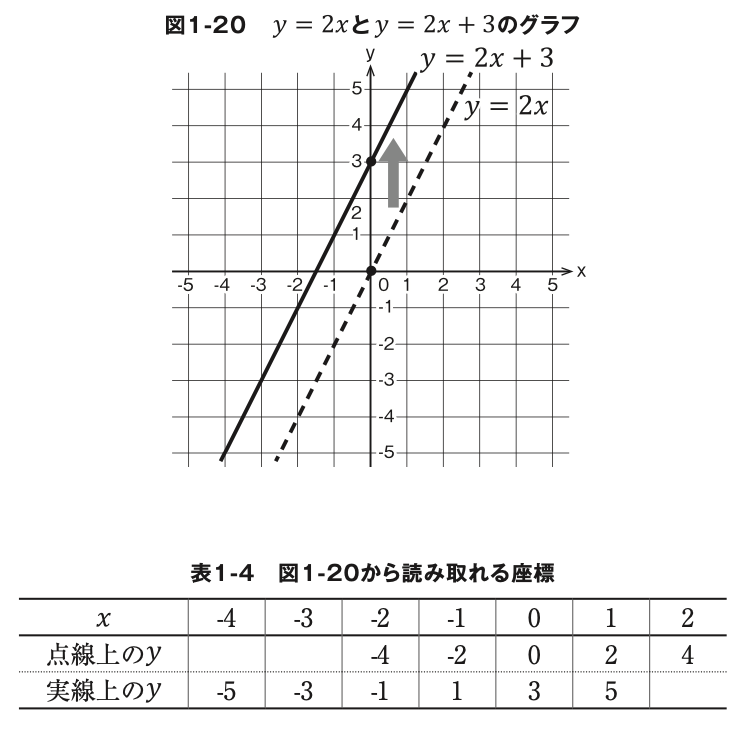
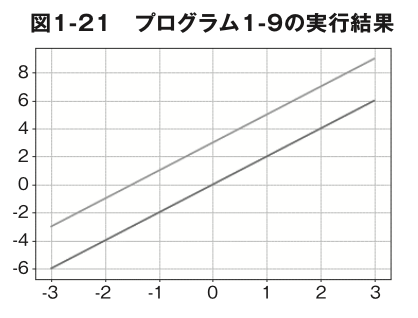
図 1 – 20のグラフをプログラムで描いてみましょう。プログラム1 – 9 は、 y=2xと y=2x+3のグラフを同じプロットに描画するプログラムです。
プログラム1 – 9
def func_6a(x):
return 2 * x
def func_6b(x):
return 2 * x + 3
x=[]
y1 = []
y2 = []
for i in range(-3, 4):
x.append(i)
y1.append(func_6a(i))
y2.append(func_6b(i))
plt.plot(x, y1)
plt.plot(x, y2)
plt.grid(color=’0.8′)
plt.show()
実行結果(図 1-21)を見ると図 1-20 と傾きが違いますが、これは plt.axis(‘equal’) を省略したからです。グラフの目盛りで変化の割合を調べると、傾きはどちらも 2 で間違いありませんね。
直線を表す式
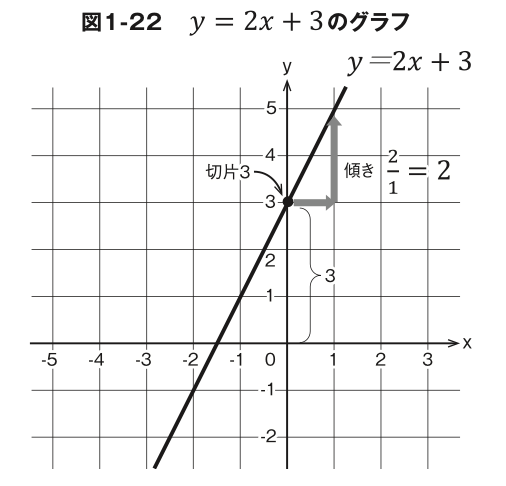
直線が y 軸と交わる点を「切片」と言います(図 1-22)。ここで直線の傾きをa、切片をbとすると平面上の直線はすべて
y=ax+b. ―式❸
で表すことができます。なお、切片は x=0のときの yの値ですから、
原点からの距離と同じことです 。つまり 、式 ❸ は「 y=axの直線をy軸 の方向にbだけ平行移動する」という意味です。 b<0のときは原点 よりも下に移動します。
では、図 1-23 の実線はどうでしょう? 点線を x 軸方向に平行移動 したもののように見えますが、これも実は y 軸方向への平行移動です。 その証拠に図 1-23 の実線をどんどん伸ばしていくと、やがて y 軸と交 差しますね。
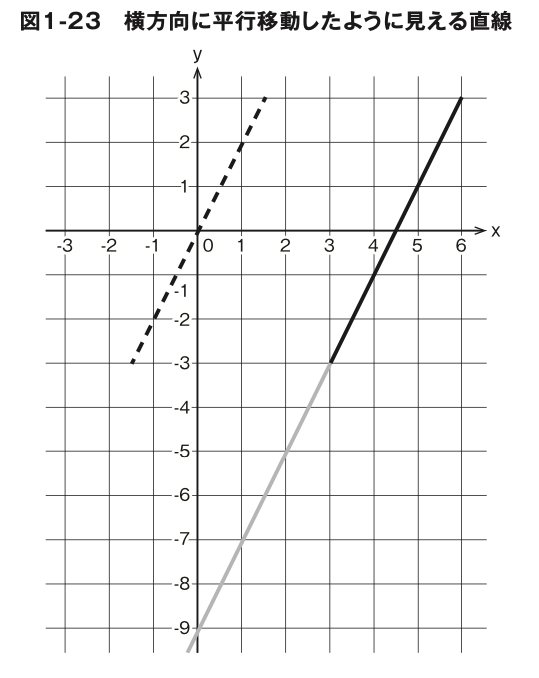
図 1-23 の点線は傾きが 2 で切片が 0 ですから、前ページの式❸で表すとy=2xになります。実線のほうは傾きが 2 で切片が -9 ですから、 同様にy=2x-9と表せます。
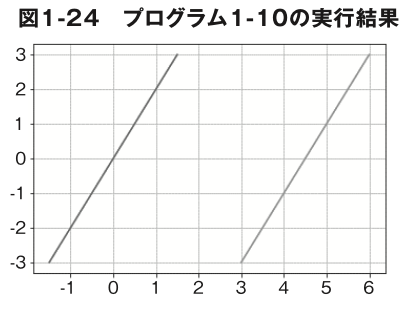
プログラム 1-10 はこれらの式を使ってグラフを描画するプログラ ムです。x の範囲を工夫すると、図 1-24 のように横方向に平行移動したような直線を描画できます。
プログラム 1-10
import numpy as np
def func_7a(x):
return 2 * x
def func_7b(x):
return 2 * x -9
x1 = np.arange(-1.5, 2)
y1 = func_7a(x1)
plt.plot(x1, y1
x2 = np.arange(3, 7)
y2 = func_7b(x2)
plt.plot(x2, y2)
plt.grid(color=’0.8′)
plt.show()
NumPyを使ってプログラムをすっきりと
プログラム 1-10 のプログラムですが、これまでよりもすっきりしたと思いませんか?
これまでは Python のリスト型の変数に複数のxとyの値を入れていましたが、プログラム1-10ではNumPyモジュールの配列を使いました。これを使うと、とても効率よく数値演算を行うことができます。数学の勉強用にPython を選んだ理由のひとつがここに現れています。
では、プログラムをくわしく見ていきましょう。
1 行目は NumPy モジュールのインポートです。このように NumPy は「np」という名前で読み込むのが慣例になっています。3 ~ 9 行目は これまでのプログラム同様、直線の式を関数で定義したものです。
12 行目x1 = np.arange(-1.5, 2)を見てください。これは、NumPy の配列に値を代入する命令 です。NumPy モジュールの arange() は、range() と同じように指定した 区間の連続する数値を作る命令です。たとえば、
x1 = np.arange(-1.5, 2)
のように引数を設定すると、配列 x1 には -1.5 から 2 まで、1 刻みで連続 する値、つまり[-1.5, -0.5, 0.5, 1.5]*6が代入されます。これをx座標とし て対応する y 座標を計算しているのが 13 行目の
y1 = func_7a(x1)
です。この1行で配列 x1 のすべての要素に対して func_7a() を実行し、 その戻り値である[-3, -1, 1, 3]を配列y1に代入します。14行目は得られ た座標を使ってグラフを描画する命令です。
同じように、17 ~ 19 行目は 2 本目のグラフを描く命令です。これまで Python のリスト型の変数を使って、
x2 = []
y2 = []
for i in range(3, 7):
x2.append(i)
y2.append(func_7b(i))
といったように書いていた部分が、NumPy の配列を使うと
x2 = np.arange(3, 7)
y2 = func_7b(x2)
とたった 2 行で済んでしまいました。for ループを使うよりもプログラムが簡単になって、何をしているのかがわかりやすくなりましたね。
直線の式の求め方
パソコンやスマートフォンのアプリを使って直線を引く場面を想像 してください。描きたい位置に指を置いて(パソコンだったらマウス の左ボタンを押して)、そのまま終点まで動かして指を離す─ こん な感じですね。この直線も数式で表すことができるでしょうか? 答 えはもちろん「Yes」です。ただ、そのためにはちょっとだけ計算が必要です。
方程式とは、 3+x=10のように文字を含んだ等式です。この等式 が成立するような の値を求めることを「方程式を解く」と言い、求めたxの値を「方程式の解」と言うのですが、実はグラフを描くだけで 方程式の解が求められるのです。直線を様々な面から理解するために、 ここではグラフから方程式を解く方法について見てみましょう。
関数と方程式
図 2-1 は、関数 のグラフです。 xの値が決まれば、 yの値は 表 2-1 に示すように 1 つに決まりますね。未知数を左辺に移項して式を整理すると という方程式になります。この方程式の解の集まりが、図 2-1(表 2-1) だということに気付いたでしょうか?
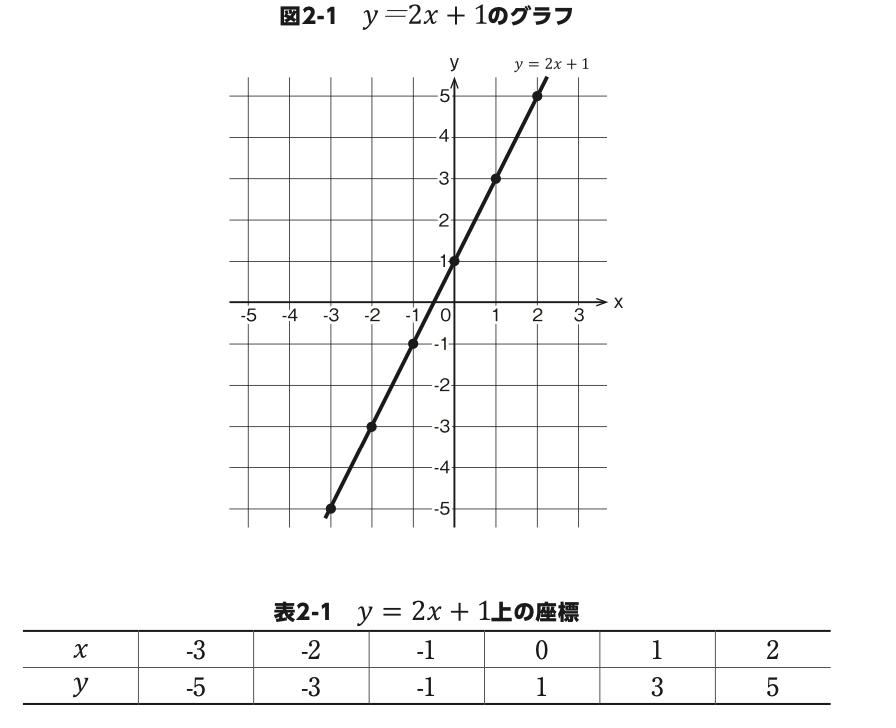
式に含まれる文字に、ある特定の値を入れたときだけ等式が成立す るのが方程式です。 y=2x+1も、xとyの値が表2-1の組み合わせのときだけ等式が成立することから、 y=2x+1を「直線の方程式」のように呼ぶこともあります。
次に、こんな問題を考えてみましょう。 太郎くんの家から公園までは2100mです。この道のりを1分間に 70m の速さで休みなく歩くとしましょう。歩きはじめからの経過時間 (単位は分)を とすると、公園までの残りの距離(単位はm) は
y=2100-70x
で求められますね。プログラム 2-1 は、この式を使ってグラフを描画するプログラム、図 2-2 は実行結果です。
プログラム2-1
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np |
def func(x):
return 2100 – 70 * x
x = np.arange(0, 60)
y = func(x)
plt.grid(color= ‘0.8’)
plt.show()
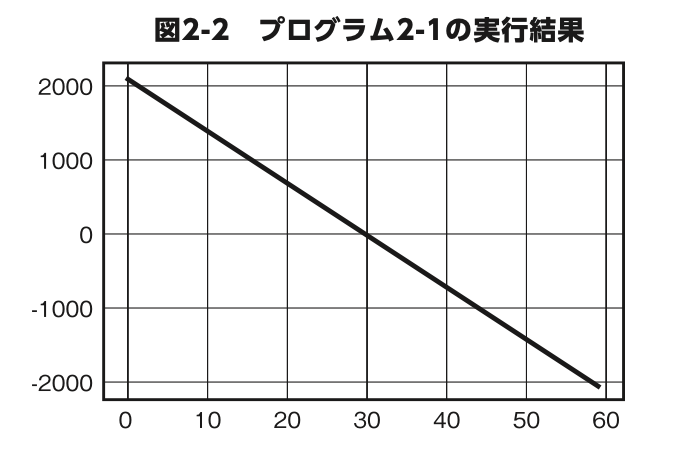
図 2-2 で注目してほしいのは、直線が x 軸( )と交わる点です。
このときの座標が何を表しているのかわかりますか? それを考えるために、少し視点を変えて次の方程式を解いてみましょう。
2100-70x=0
これを解くには、左辺が を含んだ項だけになる ように 2100 を右辺に移動します。
-70x=-2100
両辺ともにマイナスなので、これを外して
70x=2100
ここまで来れば、あとは
x=30
と、簡単ですね。 これを「移項」と言います。
ここで解いた方程式はy=2100-70x の、 yを0にしたもので す。図2-2でいうと、直線がx軸と交わる点の x座標を求める式です。
y=2100-70xは公園までの残りの距離を求める関数ですから、その 答えが 0 になるのは公園に到着したときです。つまり、直線が x 軸と交 わる点の x座標は、歩き始めてから到着までにかかる時間ということ になります。
SymPyで計算する
y=2100-70xのように簡単な方程式なら暗算でも解を求められ ますが、複雑な方程式は代数計算用の SymPy モジュールを使って解きましょう。方程式も扱える便利な計算機として手軽に Python を使 えるようになれば、数学の勉強もはかどります。
式を定義する
先ほどと同じ問題をもう一度考えてみましょう。
太郎くんが 2100m 離れた公園に向かって1分間に70mの速さで休みなく歩くとき、ス タートしてからの経過時間(単位は分)をx とすると、残りの距離(単位はm) yは y=2100-70xで求められますね。たとえば 10 分間歩いたときの残りの距離は、 xに 10 を代入して計算すると
y=2100-70×10
y=1400
1400mとわかります。SymPyを使ったプログラムで、これと同じ計 算をコンピュータにやらせてみましょう。プログラム 2-2 は、方程式 を定義するプログラムです。
プログラム2-2 SymPyで方程式を定義する
import sympy as sp
x = sp.Symbol(‘x’)
y = 2100 – 70 * x
y
1 行目は SymPy モジュールをインポートする命令です。モジュール 内の命令を呼び出しやすいように「sp」という名前を付けました。3 行目の Symbol(‘x’) は、式の中で使う記号を定義する命令です。この例では歩き始めからの経過時間を xとして式を立てるので、
x = sp.Symbol(‘x’)
のように命令を実行してください。
4 行目が計算式の定義です。文字式では掛け算の×を省略して「 70x」のように書きますが、プログラムでは掛け算の記号は省略できませ ん。これで変数 y には式の右辺が代入されます。5 行 目では変数 y の内容を確認するために、変数名だけを記述しました。 このプログラムを実行すると、
2100-70x
のように を含んだ文字式が表示されます。
Jupyter Notebookには MathJax という数学のための表示エンジンが組み込まれているので、 SymPy で定義した数式は数学の教科書で見るような読みやすい形で 表示されます。
文字式の書き方
あらためて説明するまでもないかもしれませんが、文字式とは
値を代入する 今度は定義した式中の記号に値を代入してみましょう。プログラム 2-2 を実行したあとに新しいセルを追加して、次の命令を入力し、実行してみてください。
In [3] : ans = y.subs(x, 10)
ans
Out [3] : 1400
1行目のy.subs(x, 10)は、「yが指す式中のxに10を代入する」という 意味です。変数 y が指す式とはプログラム 2-2 の 4 行目で定義した式ですから、その式の に10を代入するととなり、その計算結果が変数 ans に代入されるというしくみです。
いかがですか? 式を定義してから答えが出るまで、プログラムに するとほんの数行です。「いやいや、暗算の方が早いでしょう」という のは早合点ですよ。SymPy を使うと連立方程式の解も一瞬で求められ ます。
変数の値を画面に表示する
プログラム 2-2 の 5 行目やこの ans のように、セルの最後に変数名を 書いて実行すると、その変数の値がセルの直下に Out[ 履歴番号 ] とし て表示されます。ここで注意してほしいのは「セルの最後に」という 部分です。試しに 1 つのセルに書いて実行すると、図 2-3 のように変数 ans の値しか表示されません。

セルの途中、別の言い方をすると、プログラムの途中で変数の値を出力するときは print( ) を使います。この場合、文字式は図 2-4 上のよう にプログラムに書いた計算式と同じ形で表示されます。図 2-4 下のように出力するには、display( )を使用してください。

複数の文字を含んだ式
半径 rの円の面積は πrの2乗で求められますね。プログラム2-3 は、この 公式を定義するプログラムです。SymPy モジュールには円周率 が 「pi」としてあらかじめ定義されています。プログラムで新たに変数として定義するのは半径の「r」だけです(1 行目)。
プログラム2-3 円の面積の公式
r = sp.Symbol(‘r’)
expr = sp.pi * r**2
display(expr)
プログラム 2-3 を実行すると
πrの2乗
が表示されます。数式は英語で expression、これを省略して expr という名前の変数に式を代入しました。
記号に値を代入するときに使う subs( ) の語源は substitution(代入)です。 この式には πとr 、2 つの文字が含まれていますね。こ こに具体的な値を代入して計算するには、subs( )の引数をPythonの ディクショナリ型で指定します。プログラム 2-3 を実行してから次の 命令を実行すると、半径が 5 の円の面積を円周率 3.14 で計算するこ とができます。
In [5] : expr.subs({sp.pi:3.14, r:5})
Out [5] : 78.5
(x , y )を 通 っ て 傾 き が の 直 線 の 式
さて、SymPyの使い方がわかったところで、直線の話に戻りま しょう。パソコンやスマホのアプリを使って描いた直線も、ちゃんと y=ax+bで表すことができます。「傾きも切片もわからないのにどう やって?」と思うかもしれませんが、これらの値は直線の始点と終点の座標から求めることができます。順番に見ていきましょう。
切片bの求め方
直線を引くときに必要なものは「直線上の 1 点」と「直線の傾き」です。 たしかに図 2-5 を見ると、直線の傾きがこれと決まっていたら、点 A を 通る直線はこの 1 本しか引けませんね。
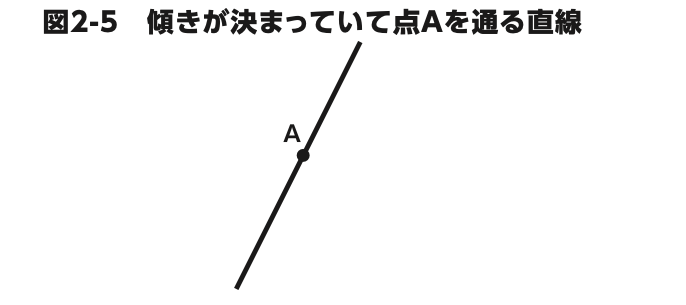
特別な場合を除くと、平面上の直線は式 ❶で表すことができます。
y=ax+b─ 式❶
いま、図2-5の傾きを2、点Aの座標を(3, 4)として式❶に代入すると
4=2×3+b
で す。この式を解くとb=-2ですから、図2-5の 直線の式は
y=2x-2
となります。
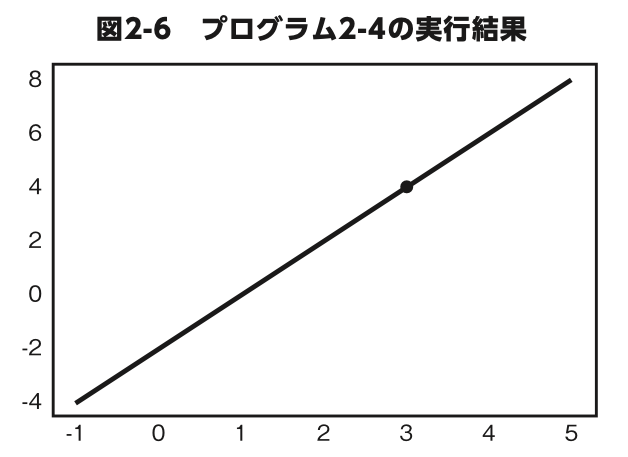
プログラム 2-4 は のグラフを描画するプログラムです。
Matplotlib.Pyplotモジュールのscatter()を使って、(3, 4)の位置に点も 描画しました。このプログラムを実行すると、図 2-6 のようになります。
図 2-5 とは傾きが違いますが、これはプロットの縦横比が 1:1 ではないからです。座標軸の目盛りを読み取って変化の割合を見ると、傾きは 2で間違いありませんね。
プログラム2-4 (3,4)を通って傾きが2の直線(
def func(x):
return 2 * x – 2 # 3.
x = np.arange(-1, 6) 5.y = func(x)
plt.plot(x, y)
plt.scatter(3, 4)
plt.show()
座標軸を描画する
Matplotlib にデータを与えると、自動的に座標軸の範囲や目盛りの 大きさを調整して、図 2-6 のようにデータ全体を収めたきれいなグラフを描画してくれます。とはいえ、このグラフを見せられて「傾きは 2 で間違いありません」と言われても、すぐには納得できないと思います。
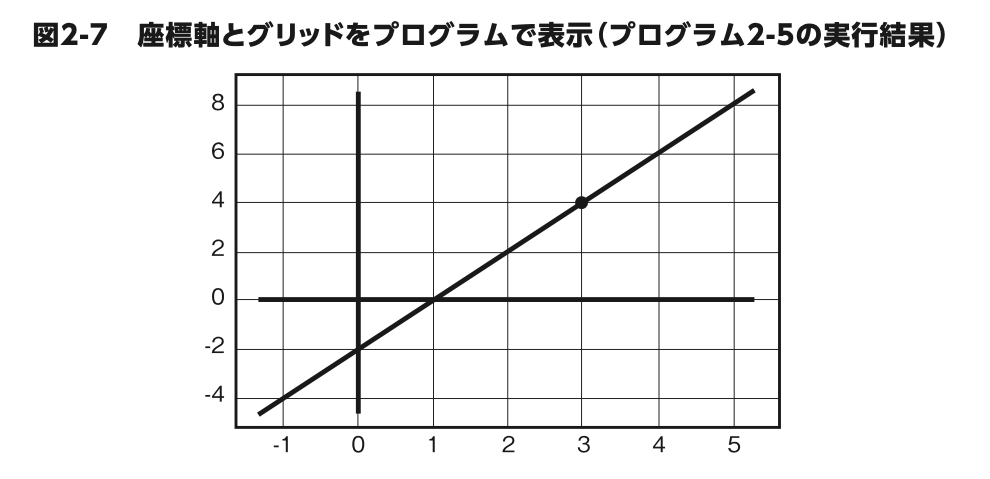
では、図 2-7 ならどうですか?
グリッドを表示して、さらに x 軸と y 軸を追加しただけですが、これなら傾きも切片も、一目でわかります ね。
プログラム 2-5 は、プログラム 2-4 と同じグラフに座標軸とグリッド を追加するプログラムです。
プロットするデータ x と y には値が 代入されていることが前提です。必ずプログラム 2-4、プログラム 2-5 の順番にプログラムを実行してください。
プログラム2-4 (3,4)を通って傾きが2の直線(
def func(x):
return 2 * x – 2 # 3.
x = np.arange(-1, 6) 5.y = func(x)
plt.plot(x, y)
plt.scatter(3, 4)
plt.show()
プログラム2-5 座標軸を表示する
plt.plot(x, y)
plt.scatter(3, 4)
xmin, xmax, ymin, ymax = plt.axis() 5. plt.hlines(0, xmin, xmax)
plt.vlines(0, ymin, ymax)
plt.grid(color=’0.8′)
plt.show()
プログラム 2-5 の 4 行目の plt.axis() は、現在のグラフから座標値の範 囲を取得する命令です。
xmin, xmax, ymin, ymax = plt.axis()
のように記述すると x 軸の最小値と最大値、y 軸の最小値と最大値の 順に取得できます。これらの値はプロットするデータから自動的に計 算されます。
5行目の
plt.hlines(0, xmin, xmax)
は水平線を描画する命令です。先頭の引数は水平線を描画する y の位 置、2番目と3番目の引数はxの範囲です。
上記のように引数を与えるとy=0の位置、つまりx軸の位置に水平線を描画します。6行目の vlines() は垂直線を描画する命令です。
こちらも先頭の引数は 0 なので、 この場合は x=0、つまり y 軸の位置に y 軸の最小値から最大値の範囲 で描画します。 プログラム 2-5 では水平線と垂直線を 1 本ずつしか描画しませんでしたが、これらの命令が hlines()、vlines() のように複数形になっている ことに気付きましたか?
次のように y 座標と描画色をリストで与え ると、4 本の水平線をそれぞれ色を変えて描画できるので試してみて ください。
plt.hlines([0, 2, 4, 6], xmin, xmax, colors=[‘k’,’r’,’g’,’b’])
公式を利用する
平面上の直線の式は
❶ y=ax+b
で表せることはすでに説明しました。ここに点 A の座標 ( x1,y1)を代入すると
❷ y1=ax1+b
と書けます。ここで2つの式からbを消すために「❶-❷」を計算しま しょう。左辺、右辺それぞれで❶から❷を引いて、そこから式を整理す ると
y-y1=ax+b-(ax1+b)
y-y1=ax+b-ax1-b
y=a(x-x1)+y1 式❸
となり、これが点A( x1,y1)を通って傾きaの直線を表す式になります。
先ほどは切片を求めてから直線の式を求めましたが、最後の式❸を使えば傾きと点 A の座標を入れるだけで求められます。 たとえば、(3, 4)を通って傾きが2の直線の式は
y=2(x-3)+4
y=2x-2
となります。
SymPyを使って計算する
直線上の1点と傾きがわかっていれば、式y=a(x-x1)+y1❸に値を代入して式を整理することで、 y=ax+bの形の直線の式が求められることがわかりました。難しい計算ではありませんが、ちょっとだけ面倒ですね。そこで、SymPy モジュールにこの式を整理してもらいましょう。
プログラ ム2-6は、式❸をもとに傾きが2で(3, 4)を通る直線の式を求めるプロ グラムです。
プログラム2-6 傾きが2で(3, 4)を通る直線の
x = sp.Symbol(‘x’)
a = sp.Symbol(‘a’)
x1, y1 = sp.symbols(‘x1, y1’)
y = a * (x-x1) + y1
y = y.subs({a:2, x1:3, y1:4})
y
1 ~ 3 行目は式で使う記号の定義です。直線上の点の座標を表す記号x1、y1は3行目で2つ同時に定義しました。この場合はSymbol()で はなく symbols() を使うので注意してください。
その次に 5 行目で式y=a(x-x1)+y1❸を定義しておき、6 行目の y = y.subs({a:2, x1:3, y1:4}) は、式中の傾きと座標に具体的な値を代入して式を書き換える命令で す。このプログラムを実行すると、 2x-2のように直線の式が表示されます。
SymPyでグラフを描く
SymPy を使ってできることは文字式の計算処理だけではありませ ん。 sp.plot(y) と、たったこれだけで、yが指す式(ここでは 2x-2 )を使ったグラフが 描画できます(図 2-8)。
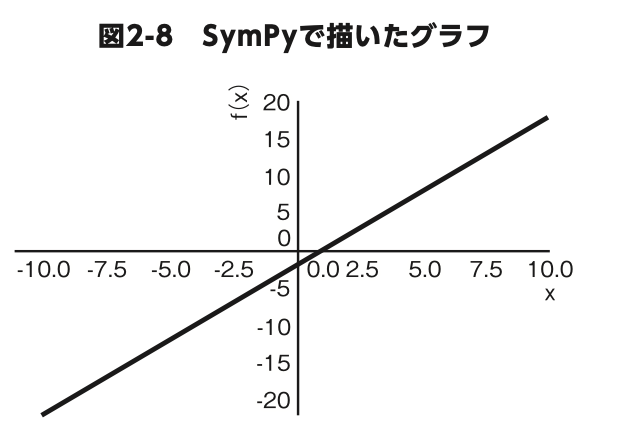
Matplotlib のグラフとは違って、SymPy のグラフには座標軸と軸のタイトル(横軸はx、縦軸はyの関数を表すf(x))が表示されます。また、 横軸xの範囲は標準では-10 から10です。この範囲はsp.plot()の2つ目の引数で変更できます。
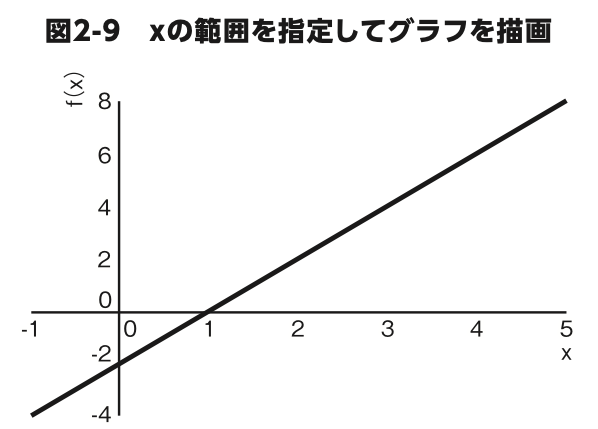
たとえば、-1から5 の範囲のグラフを描画するには、
sp.plot(y, (x, -1, 5))
のように引数を指定してください(図 2-9)。
2点を通る直線の式
点が 1 つだけ与えられたとき、その点を通る直線は何本も引くこと ができますが、点が2つになると、その2点を通る直線は 1 つに決まり ます。今度は 2 つの座標から直線の式y=ax+b を求めてみましょう。
直線の傾きを求める
2 つの点が与えられたとき、その 2 点を通る直線は 1 つしかありません(図 2-10)。
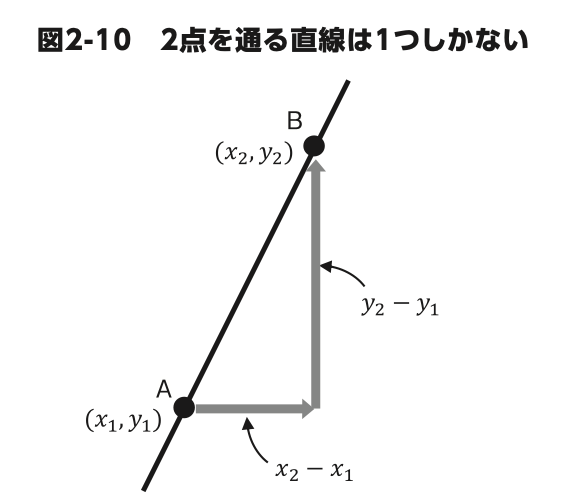
直線の傾きは「変化の割合」を表しているので、式

を使えば求められますね。それぞれの増加分は 2 点の座標を引き算すればよいので、点Aの座標を( x1,y1)、点Bの座標を(x2,y2 )とすると、 図2-10の直線の傾きaは
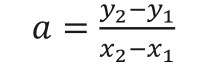
で表せます。これを直線上の 1 点と傾きが与えられたときの式
y=a((x-x1)+y1 式❸
に代入すると、
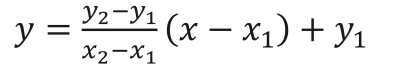
式❹ となり、これが与えられた 2 点を通る直線の式になります。では、x1=x2 はどのような直線かというと、それ は x 軸の を通って y 軸に平行な直線になります。
図 2-11 を見てください。(1,0) と (3,4) を通るこの直線は傾きが 2、切片 は -2 ですから、この直線の式は で間違いありませんね。では、式❹で図 2-11 の直線の式が求められるのか確認しましょう。もちろん、 計算は SymPy にまかせます。
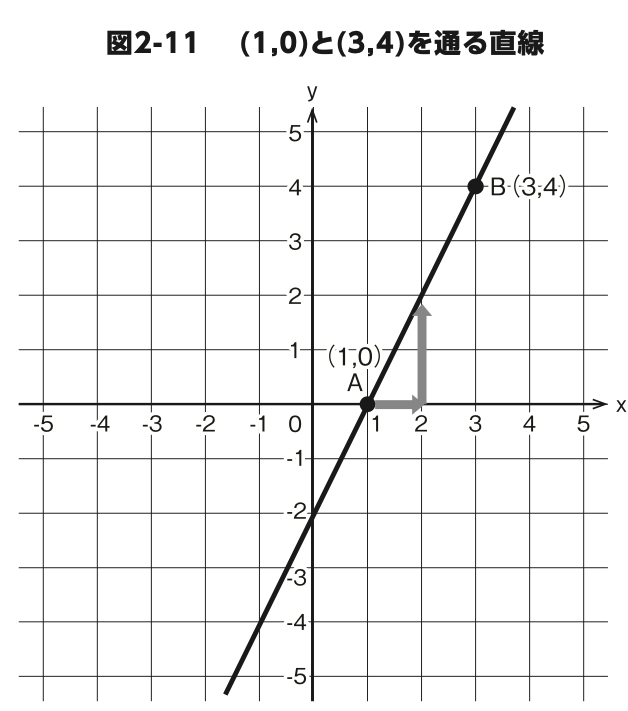
プログラム2-7は、(1, 0)と(3, 4)の2点を通る直線の式を求めるプログ ラムです。このプログラムを実行すると、グラフから読み取った直線の 式と同じ
2x-2
が表示されるはずです。
プログラム2-7 2点を通る直線の式
x = sp.Symbol(‘x’)
x1, y1 = sp.symbols(‘x1, y1’)
x2, y2 = sp.symbols(‘x2, y2’)
y=((y2-y1)/(x2-x1)) * (x-x1) + y1
y = y.subs({x1:1, y1:0, x2:3, y2:4})
y
5 行目で式❹
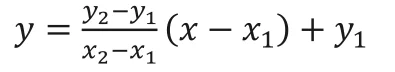
を定義しているのですが、もとの式よりも複雑に見え ますね。これは正しい順番で計算されるように( )を追加したから です。このプログラムをもう少しくわしく見ていきましょう。
1 つの式に足し算・引き算・掛け算・割り算が含まれている計算を するときは、掛け算・割り算を先にしてから足し算・引き算を計算し ますね。このルールはプログラムでも同じで、Python では表 2-3 に示すように優先順位が決まっています。また、式中に( )があるときは ( )の中を先に計算するというルールもプログラムで通用します。
以上を踏まえて、式❹
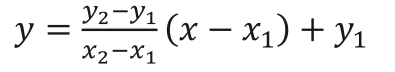
とプログラム 2-7 の 5 行目 y=((y2-y1)/(x2-x1)) * (x-x1) + y1 を見比べてください。分数はプログラムの中では割り算になるので この部分を y2-y1 / x2-x1 ── ❸のように書きたくなりますが、これでは思った通りの計算はできませ ん。この書き方だとコンピューターは、
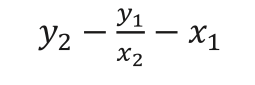
という計算をしてしまいます。 は変化の割合を求める式ですから、割り算の前に分子および分母を計算しなければいけません。そのためには引き算を( )で囲む必要があります。

連立方程式を使って2点を通る直線の式を求める
直線上の 2 点がわかっているときは、式❹
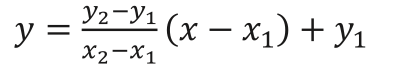
で直線の式を求められるのですが、この式を覚えておくのは大変です。 でも、 y=ax+b
ならもう自然と頭に焼き付いているのではないでしょうか。この式に点Aの座標(1, 0)を代入すると
0=a+b ─⑤
点Bの座標(3, 4)を代入すると
4=3a+b. ─⑥
になります。2つの式から を消すために「⑥-⑤」を計算しましょう。 左辺と右辺それぞれで6から5を引いて式を整理すると、
4-0=3a+a-(a+b)
a=2
となって、直線の傾きa が求められました。これを5に代入すると b=-2のように切片 が求められます。よって、(1, 0)と(3, 4)を通る直線の式は y=2x=2です。プログラム 2-7 の実行結果と同じ式になりました。
SymPyを使って連立方程式を解く
直線上の 2 点がわかっているときは、 y=ax+bにそれぞれの座標 を入れて式を 2 つ作り、これを連立方程式として解くと直線の式が求 められます。たとえば、直線が(1, 0)と(3, 4)を通る場合は
0=a+b
4=3a+b
のように式を立てます。簡単な計算ですが、暗算では難しい。紙と鉛筆 を用意し、自分で式を書いて……となると面倒ですね。 プログラム 2-8 は SymPy を使って連立方程式を解くプログラムで す。1 ~ 2 行目は記号の定義、4 ~ 5 行目は式の定義、その後の 7 行目が 連立方程式を解く命令です。
プログラム2-8 連立方程式を解く
a = sp.Symbol(‘a’)
b = sp.Symbol(‘b’)
expr1 = a + b
expr2 = 3 * a + b – 4
ans = sp.solve([expr1, expr2])
ans
式を定義するときは、左辺(または右辺)が 0 に なるように式を整理してください。2 つの式をリストにして ans = sp.solve([expr1, expr2]) のように solve( ) に渡すだけで連立方程式が解けます。驚くほど簡単で しょう?
プログラムを実行すると
{a: 2, b: -2}
のように 2 つの解が表示されます。波括弧{ }は Python のディクショ ナ リ 型 を 表 し て い る の で 、そ れ ぞ れ の 解 は キ ー を 使 っ て a n s [ a ] 、a n s [ b ] で参照できます。
2直線の交点
平面上にある 2 本の直線は、平行でない限り必ずどこかで交わります(図2-13)。
この交点の座標を求めるにはどうすればいいと思 いますか?
関数のグラフは方程式の解の集まりだという話をしました。これをヒントに 2 本の直線の交点が何を表しているか、少し考えてみてください。
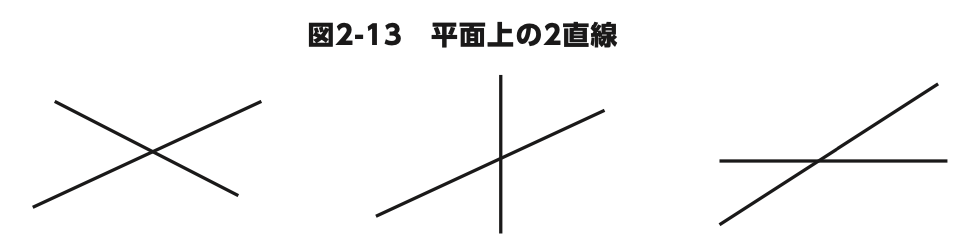
直線の式を使ってグラフが描けることは確認済みですね。このグラフは直線の式を整理して作った方程式の解の集まりです。
そして 2 つの直線が交わるのですから、2 つの方程式は同じ解を持つ、 つまり、連立方程式の解が 2 直線の交点ということになります。
交点が表すもの
太郎くんと二郎くんは二人とも家にいましたが、太郎くんが先に 1 分間に 70m の速さで家から公園に向かって歩き始めました。置いてき ぼりにされた二郎くんは、太郎くんが出発してから 6 分後に自転車に 乗って、1 分間に 100m の速さで同じ道を追いかけました。
さて問題で す。二人の速さが変わらないとき、太郎くんが家を出てから何分後に 二郎くんは追いつけるでしょうか?
むかし懐かしい旅人算です。 解き方を覚えていますか?
太郎くんが家を出てから 6 分間に進む距離は 70m × 6 分で 420m。速 さから計算すると、二人の距離は 100m – 70m で 1 分間に 30m 縮まる。420m の差が 0 になるには 420m ÷ 30m で 14 分かかる。
求めるのは太郎くんが出発してからの時間だから、6 分+ 14 分で答えは 20 分後です。
答えがわかったところで、図 2-14 を見てください。これは太郎くん が家を出発してからの時間と、二人の家からの距離の関係をそれぞれ グラフにしたものです。実線は太郎くん、点線は二郎くん、そして求め る答えは二人のグラフが交わるところです。
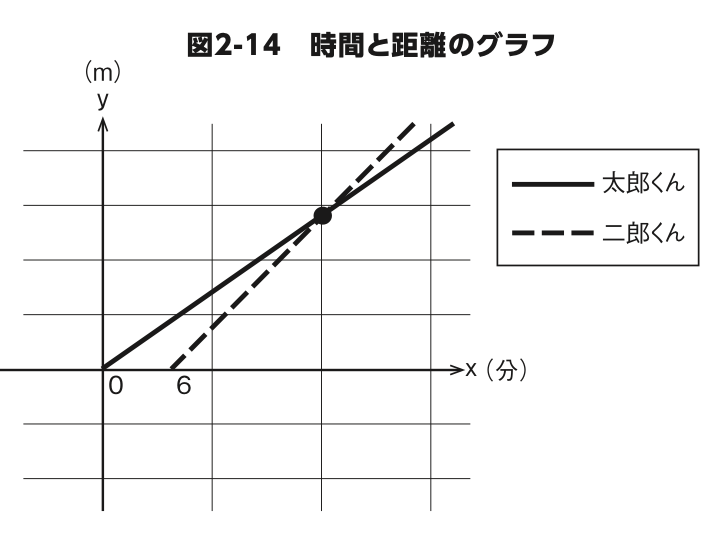
x 軸 は 時 間(単 位 は 分)、y 軸は距離(単位は m)です。太郎くんは 1 分間に 70m の速さで進むのですから、 実線で表された直線の式は
y=70x
で間違いありませんね。問題は二郎くんです。1 分間に 100m 進むので すから傾き は 100 ですが、切片 がわかりません。しかし、太郎くん の6分後にスタートするのですから、この直線が(6, 0)を通ることはわ かっています。ということは、
y=a(x-x1)+y1─ 式❸の式を使えば二郎くんの式が求められますね。
プログラム 2-10 は二郎くんの直線の式を求めるプログラムです。このプログラムを実行すると、
100x-600
が表示されます。
プログラム2-10 傾きが100で(6, 0)を通る直線の式
x = sp.Symbol(‘x’)
a = sp.Symbol(‘a’)
x1, y1 = sp.symbols(‘x1, y1’)
y = a * (x-x1) + y1
y = y.subs({a:100, x1:6, y1:0})
y
2直線の交点と連立方程式の解
太郎くんと二郎くんの直線は、それぞれ次の式で表されることがわかりました。
y=70x
y=100x-600
これを連立方程式として解くと、直線の交点の座標がわかります。 SymPy を使って計算しましょう。
プログラム2-11 直線の交点を求める
x = sp.Symbol(‘x’)
y = sp.Symbol(‘y’)
expr1 = sp.Eq(y, 70*x)
expr2 = sp.Eq(y, 100*x-600)
ans = sp.solve([expr1, expr2])
ans
プログラム 2-11 を実行すると、
{x: 20, y: 1400}
のように答えが 2 つ表示されます。これが 2 つの直線の交点の座標、つまり太郎くんと二郎くんが会う点です。
x 軸は時間(単位は分)、y 軸は距離(単位は m)ですから、2 人が会うのは太郎くんが出発してから 20 分後、スタート地点から 1400m の場所ということがわかります。
SymPyでグラフを描く
SymPyを使えばプログラムで定義した式からグラフが描ける話をしました。しかし、プログラム 2-11 の 4 ~ 5 行目で定義した式
expr2 = sp.Eq(y, 100*x-600)
ans = sp.solve([expr1, expr2])
では、グラフを描くことはできま せん。Eq( ) を使って定義した式は方程式であり、関数ではないか らです。 グラフを描く場合は、 sp.plot(70*x, 100*x-600, (x, 0, 30)) のように引数を設定してください。最初の引数は太郎くんの直線の式、 2 番目の引数は二郎くんの直線の式、3 番目の引数は座標の範囲です。 このように複数の式を渡すと、同じプロットにグラフを描画できます (図 2-15)。
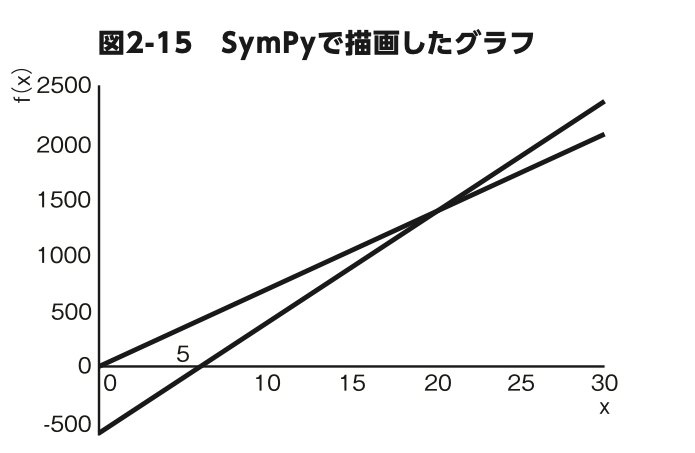
もう一度、この節の最初に戻って旅人算の解き方を見てみましょう。
このときは太郎くんが出発したあと、二郎くんが追いつくまでにかかる時間はわかりましたが、それがどの地点かということはわかりませ んでした。しかし、グラフを描いてみると、2 人がいつ、どこで会うの かひと目でわかります。その答えはもちろん 2 つの直線が交わる点です。
